【題目】將余弦函數的圖象向右平移
個單位后，再保持圖象上點的縱坐標不變，橫坐標變為原來的一半，得到函數
的圖象，下列關于的敘述正確的是（ ）
A. 最大值為
，且關于
對稱
B. 周期為
，關于直線
對稱
C. 在
上單調遞增，且為奇函數
D. 在
上單調遞減，且為偶函數
科目：高中數學 來源： 題型：
【題目】
已知
是遞增數列，其前
項和為
，
，且
，
．
（Ⅰ）求數列的通項
；
（Ⅱ）是否存在
使得
成立？若存在，寫出一組符合條件的
的值；若不存在，請說明理由；
（Ⅲ）設
，若對于任意的
，不等式
恒成立，求正整數
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，已知曲線C的極坐標方程為
＝
（
＞0），過點
的直線
的參數方程為
（t為參數），直線與曲線C相交于A，B兩點．
（Ⅰ）寫出曲線C的直角坐標方程和直線的普通方程；
（Ⅱ）若
，求的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某校隨機抽取100名學生，獲得了他們一周課外閱讀時間（單位：小時）的數據，整理得到數據分組及頻數分布表和頻率分布直方圖：
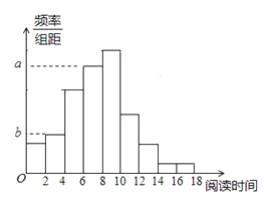
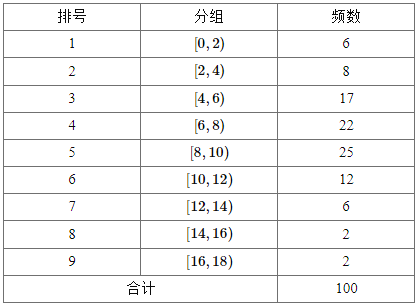
（1）求頻率分布直方圖中的
，
的值；
（2）從閱讀時間在
的學生中任選2人，求恰好有1人閱讀時間在
，另1人閱讀時間在
的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】四棱錐
中，
平面
，底面四邊形為直角梯形，
，
，
，
.
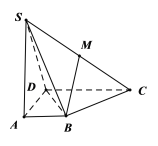
（Ⅰ）求證：平面
平面
；
（Ⅱ）求二面角
的余弦值；
（Ⅲ）
為
中點，在四邊形所在的平面內是否存在一點
，使得
平面
，若存在，求三角形
的面積；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知長方形
中，
，
，現將長方形沿對角線折起，使
，得到一個四面體
，如圖所示，
（1）試問：在折疊的過程中，異面直線
與
能否垂直？若能垂直，求出相應
的值；若不垂直請說明理由；
（2）當四面體體積最大時，求二面角
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
