
【題目】已知函數![]() 曲線
曲線![]() 在原點處的切線為
在原點處的切線為![]() .
.
(1)證明:曲線![]() 與
與![]() 軸正半軸有交點;
軸正半軸有交點;
(2)設曲線![]() 與
與![]() 軸正半軸的交點為
軸正半軸的交點為![]() ,曲線在點
,曲線在點![]() 處的切線為直線
處的切線為直線![]() ,求證:曲線
,求證:曲線![]() 上的點都不在直線
上的點都不在直線![]() 的上方 ;
的上方 ;
(3)若關于![]() 的方程
的方程![]() (
(![]() 為正實數)有不等實根
為正實數)有不等實根![]() 求證:
求證:![]()
【答案】(1)見解析(2)見解析(3)見解析
【解析】分析:(1)由條件可得![]() ,然后利用單調性及零點存在定理可得存在
,然后利用單調性及零點存在定理可得存在![]() 使得
使得![]() ,從而得結論成立.(2)由(1)可得曲線
,從而得結論成立.(2)由(1)可得曲線![]() 在點
在點![]() 處的切線
處的切線![]() :
:![]() . 令
. 令![]() ,
,![]() ,則
,則![]() ,由
,由![]() 的單調性可得
的單調性可得![]() ,從而可得結論成立.(3)結合以上兩問中的有關結論構造新的函數進行證明可得結論成立.
,從而可得結論成立.(3)結合以上兩問中的有關結論構造新的函數進行證明可得結論成立.
詳解:證明:(1)∵![]() ,
,
∴![]() ,
,
由已知得![]() ,解得
,解得![]()
∴![]() ,
,
∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
又![]() ,
,![]() ,
,
∴存在![]() 使得
使得![]() .
.
∴曲線![]() 與
與![]() 軸正半軸有交點
軸正半軸有交點![]() .
.
(2)由(1)可得曲線![]() 在點
在點![]() 處的切線
處的切線![]() :
:![]() ,
,
令![]() ,
,![]() ,
,
則![]() ,
,
又![]() ,
,
故當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
所以對任意實數![]() 都有
都有![]() ,
,
即對任意實數![]() 都有
都有![]() ,
,
故曲線![]() 上的點都不在直線
上的點都不在直線![]() 的上方.
的上方.
(3)由(1)知![]() ,
,
所以![]() 為減函數.
為減函數.
設方程![]() 的根為
的根為![]() ,
,
由(2)可知![]() ,
,
所以![]() .
.
記![]() ,則
,則![]()
當![]() 時,
時,![]()
![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() ,單調遞減,
,單調遞減,
所以對任意的實數![]() ,都有
,都有![]() ,
,
即![]() .
.
設方程![]() 的根
的根![]() ,
,
則![]() ,
,
所以![]() .
.
于是![]()
令![]() ,
,
又![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上為增函數,
上為增函數,
又![]()
所以![]() ,
,
所以![]()


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案科目:高中數學 來源: 題型:
【題目】已知某算法的算法框圖如圖所示,若將輸出的(x,y)值依次記為(x1 , y1),(x2 , y2),…,(xn , yn),…,則程序結束時,共輸出(x,y)的組數為( ) ![]()
A.1006
B.1007
C.1008
D.1009
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C的圓心在直線上![]() ,且與直線
,且與直線![]() 相切于點
相切于點![]()
(1)求圓C的方程;
(2)是否存在過點![]() 的直線
的直線![]() 與圓C交于
與圓C交于![]() 兩點,且
兩點,且![]() 的面積為
的面積為![]() (O為坐標原點),若存在,求出直線
(O為坐標原點),若存在,求出直線![]() 的方程,若不存在,請說明理由.
的方程,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只藥用昆蟲的產卵數![]() 與一定范圍內與溫度
與一定范圍內與溫度![]() 有關, 現收集了該種藥用昆蟲的6組觀測數據如下表:
有關, 現收集了該種藥用昆蟲的6組觀測數據如下表:
溫度 | 21 | 23 | 24 | 27 | 29 | 32 |
產卵數 | 6 | 11 | 20 | 27 | 57 | 77 |
(1)若用線性回歸模型,求![]() 關于
關于![]() 的回歸方程
的回歸方程![]() =
=![]() x+
x+![]() (精確到0.1);
(精確到0.1);
(2)若用非線性回歸模型求![]() 關
關![]() 的回歸方程為
的回歸方程為![]()
![]() 且相關指數
且相關指數![]()
( i )試與 (1)中的線性回歸模型相比,用![]() 說明哪種模型的擬合效果更好.
說明哪種模型的擬合效果更好.
( ii )用擬合效果好的模型預測溫度為![]() 時該種藥用昆蟲的產卵數(結果取整數).
時該種藥用昆蟲的產卵數(結果取整數).
附:一組數據(x1,y1), (x2,y2), ...,(xn,yn), 其回歸直線![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估計為
的斜率和截距的最小二乘估計為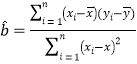 ,
,![]() ,相關指數
,相關指數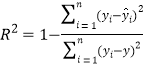 .
.
![]()
![]()
![]()
![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】綜合題。
(1)設不等式(x﹣a)(x+a﹣2)<0的解集為N, ![]() ,若x∈N是x∈M的必要條件,求a的取值范圍.
,若x∈N是x∈M的必要條件,求a的取值范圍.
(2)已知命題:“x∈{x|﹣1<x<1},使等式x2﹣x﹣m=0成立”是真命題,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)用定義證明函數![]() 在
在![]() 上是增函數;
上是增函數;
(2)探究是否存在實數![]() ,使得函數
,使得函數![]() 為奇函數?若存在,求出
為奇函數?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(3)在(2)的條件下,解不等式![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在[﹣1,1]上的奇函數,且f(1)=1,若m,n∈[﹣1,1],m+n≠0時,有 ![]() .
.
(1)解不等式 ![]() ;
;
(2)若f(x)≤t2﹣2at+1對所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求實數t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com