
【題目】已知拋物線![]() :
:![]() ,圓
,圓![]() :
:![]() ,直線
,直線![]() :
:![]() 與拋物線
與拋物線![]() 相切于點(diǎn)
相切于點(diǎn)![]() ,與圓
,與圓![]() 相切于點(diǎn)
相切于點(diǎn)![]() .
.

(1)若直線![]() 的斜率
的斜率![]() ,求直線
,求直線![]() 和拋物線
和拋物線![]() 的方程;
的方程;
(2)設(shè)![]() 為拋物線
為拋物線![]() 的焦點(diǎn),設(shè)
的焦點(diǎn),設(shè)![]() ,
,![]() 的面積分別為
的面積分別為![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() :
:![]() ,
,![]() :
:![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)第一問(wèn),一般先設(shè)出直線的方程![]() ,再根據(jù)直線和圓相切得到b的值. 再利用直線和拋物線方程組的判別式等于零,得到P的值. (2)第(2)問(wèn),一般利用函數(shù)的思想求
,再根據(jù)直線和圓相切得到b的值. 再利用直線和拋物線方程組的判別式等于零,得到P的值. (2)第(2)問(wèn),一般利用函數(shù)的思想求![]() 的取值范圍.先要分別計(jì)算出
的取值范圍.先要分別計(jì)算出![]() ,
,![]() ,從而得到函數(shù)
,從而得到函數(shù)![]() ,再選擇合適的方法求取值范圍.
,再選擇合適的方法求取值范圍.
試題解析:
(1)由題設(shè)知![]() :
:![]() ,且
,且![]() ,
,
由![]() 與
與![]() 相切知,
相切知,![]() 到
到![]() 的距離
的距離![]() ,得
,得![]() ,
,
∴![]() :
:![]() .
.
將![]() 與
與![]() 的方程聯(lián)立消
的方程聯(lián)立消![]() 得
得![]() ,
,
其![]() 得
得![]() ,
,
∴![]() :
:![]() .
.
綜上,![]() :
:![]() ,
,![]() :
:![]() .
.
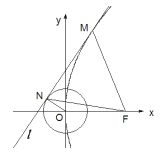
(2)不妨設(shè)![]() ,根據(jù)對(duì)稱性,
,根據(jù)對(duì)稱性,![]() 得到的結(jié)論與
得到的結(jié)論與![]() 得到的結(jié)論相同.
得到的結(jié)論相同.
此時(shí)![]() ,又知
,又知![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,
由![]() 消
消![]() 得
得![]() ,
,
其![]() 得
得![]() ,從而解得
,從而解得![]() ,
,
由![]() 與
與![]() 切于點(diǎn)
切于點(diǎn)![]() 知
知![]() 到
到![]() :
:![]() 的距離
的距離![]() ,得
,得![]() 則
則![]() ,故
,故![]() .
.
由![]() 得
得![]() ,
,
故![]()
![]()
![]() .
.
![]() 到
到![]() :
:![]() 的距離為
的距離為![]()
![]() ,
,
∴![]()
![]() ,
,
又![]() ,
,
∴![]()
![]()
![]() .
.
當(dāng)且僅當(dāng)![]() 即
即![]() 時(shí)取等號(hào),
時(shí)取等號(hào),
與上同理可得,![]() 時(shí)亦是同上結(jié)論.
時(shí)亦是同上結(jié)論.
綜上,![]() 的取值范圍是
的取值范圍是![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在直三棱柱![]() 中,
中,![]() ,
,![]() 為棱
為棱![]() 的中點(diǎn),
的中點(diǎn),![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)設(shè)二面角![]() 的正切值為
的正切值為![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點(diǎn),且
上一點(diǎn),且![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某多面體的三視圖如圖所示,則該多面體的各棱中,最長(zhǎng)棱的長(zhǎng)度為( )

A. ![]() B.
B. ![]() C. 2 D. 1
C. 2 D. 1
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 中點(diǎn).
中點(diǎn).

(1)求證:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】基因編輯嬰兒“露露”和“娜娜”出生的消息成了全球矚目的焦點(diǎn),為了解學(xué)生對(duì)基因編輯嬰兒的看法,某中學(xué)隨機(jī)從該校一年級(jí)學(xué)生中抽取了100人進(jìn)行調(diào)查,抽取的45女生中贊成基因編輯嬰兒的占![]() ,而55名男生中有10人表示贊成基因編輯嬰兒.
,而55名男生中有10人表示贊成基因編輯嬰兒.
(1)完成![]() 列聯(lián)表,并回答能否有90%的把握認(rèn)為“對(duì)基因編輯嬰兒是否贊成與性別有關(guān)”?
列聯(lián)表,并回答能否有90%的把握認(rèn)為“對(duì)基因編輯嬰兒是否贊成與性別有關(guān)”?

(2)現(xiàn)從該校不贊成基因編輯嬰兒的學(xué)生中,采用分層抽樣的方法抽取7名學(xué)生,再?gòu)谋怀槿〉?名學(xué)生中任取3人,記被抽取的3名學(xué)生女生的人數(shù)為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)![]() .
.
(1)若![]() ,試討論函數(shù)
,試討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() 有兩個(gè)零點(diǎn),求
有兩個(gè)零點(diǎn),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了調(diào)查學(xué)生數(shù)學(xué)學(xué)習(xí)的質(zhì)量情況,某校從高二年級(jí)學(xué)生(其中男生與女生的人數(shù)之比為![]() )中,采用分層抽樣的方法抽取
)中,采用分層抽樣的方法抽取![]() 名學(xué)生依期中考試的數(shù)學(xué)成績(jī)進(jìn)行統(tǒng)計(jì).根據(jù)數(shù)學(xué)的分?jǐn)?shù)取得了這
名學(xué)生依期中考試的數(shù)學(xué)成績(jī)進(jìn)行統(tǒng)計(jì).根據(jù)數(shù)學(xué)的分?jǐn)?shù)取得了這![]() 名同學(xué)的數(shù)據(jù),按照以下區(qū)間分為八組:
名同學(xué)的數(shù)據(jù),按照以下區(qū)間分為八組:
①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,⑥
,⑥![]() ,⑦
,⑦![]() ,⑧
,⑧![]()
得到頻率分布直方圖如圖所示.已知抽取的學(xué)生中數(shù)學(xué)成績(jī)少于![]() 分的人數(shù)為
分的人數(shù)為![]() 人.
人.

(1)求![]() 的值及頻率分布直方圖中第④組矩形條的高度;
的值及頻率分布直方圖中第④組矩形條的高度;
(2)如果把“學(xué)生數(shù)學(xué)成績(jī)不低于![]() 分”作為是否達(dá)標(biāo)的標(biāo)準(zhǔn),對(duì)抽取的
分”作為是否達(dá)標(biāo)的標(biāo)準(zhǔn),對(duì)抽取的![]() 名學(xué)生,完成下列
名學(xué)生,完成下列![]() 列聯(lián)表:
列聯(lián)表:

據(jù)此資料,你是否認(rèn)為“學(xué)生性別”與“數(shù)學(xué)成績(jī)達(dá)標(biāo)與否”有關(guān)?
(3)若從該校的高二年級(jí)學(xué)生中隨機(jī)抽取![]() 人,記這
人,記這![]() 人中成績(jī)不低于
人中成績(jī)不低于![]() 分的學(xué)生人數(shù)為
分的學(xué)生人數(shù)為![]() ,求
,求![]() 的分布列、數(shù)學(xué)期望和方差
的分布列、數(shù)學(xué)期望和方差
附1:“![]() 列聯(lián)表
列聯(lián)表![]() ”的卡方統(tǒng)計(jì)量公式:
”的卡方統(tǒng)計(jì)量公式:![]()
附2:卡方(![]() )統(tǒng)計(jì)量的概率分布表:
)統(tǒng)計(jì)量的概率分布表:![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐P-ABCD中,平面PAD⊥底面 ABCD,側(cè)棱PA=PD=![]() ,底面ABCD為直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O為AD中點(diǎn).
,底面ABCD為直角梯形,其中BC∥AD ,AB⊥AD,AD=2AB=2BC=2,O為AD中點(diǎn).
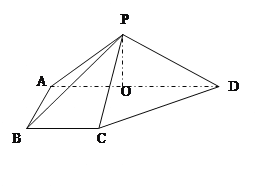
(Ⅰ)求證:PO⊥平面ABCD;
(Ⅱ)線段AD上是否存在點(diǎn)![]() ,使得它到平面PCD的距離為
,使得它到平面PCD的距離為![]() ?若存在,求出
?若存在,求出![]() 值;若不存在,請(qǐng)說(shuō)明理由.
值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司為了解廣告投入對(duì)銷售收益的影響,在若干地區(qū)各投入![]() 萬(wàn)元廣告費(fèi)用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數(shù)據(jù)丟失,但可以確定橫軸是從
萬(wàn)元廣告費(fèi)用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數(shù)據(jù)丟失,但可以確定橫軸是從![]() 開(kāi)始計(jì)數(shù)的. [附:回歸直線的斜率和截距的最小二乘估計(jì)公式分別為.]
開(kāi)始計(jì)數(shù)的. [附:回歸直線的斜率和截距的最小二乘估計(jì)公式分別為.]
(1)根據(jù)頻率分布直方圖計(jì)算圖中各小長(zhǎng)方形的寬度;
(2)試估計(jì)該公司投入![]() 萬(wàn)元廣告費(fèi)用之后,對(duì)應(yīng)銷售收益的平均值(以各組的區(qū)間中點(diǎn)值代表該組的取值);
萬(wàn)元廣告費(fèi)用之后,對(duì)應(yīng)銷售收益的平均值(以各組的區(qū)間中點(diǎn)值代表該組的取值);
(3)該公司按照類似的研究方法,測(cè)得另外一些數(shù)據(jù),并整理得到下表:
廣告投入 | 1 | 2 | 3 | 4 | 5 |
銷售收益 | 2 | 3 | 2 | 7 |
由表中的數(shù)據(jù)顯示, ![]() 與
與![]() 之間存在著線性相關(guān)關(guān)系,請(qǐng)將(2)的結(jié)果填入空白欄,并求出
之間存在著線性相關(guān)關(guān)系,請(qǐng)將(2)的結(jié)果填入空白欄,并求出![]() 關(guān)于
關(guān)于![]() 的回歸直線方程.
的回歸直線方程.


查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com