
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,兩焦點(diǎn)與短軸的一個端點(diǎn)的連線構(gòu)成的三角形面積為
,兩焦點(diǎn)與短軸的一個端點(diǎn)的連線構(gòu)成的三角形面積為![]() .
.
(I)求橢圓![]() 的方程;
的方程;
(II)設(shè)與圓![]() 相切的直線
相切的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點(diǎn)(
兩點(diǎn)(![]() 為坐標(biāo)原點(diǎn)),
為坐標(biāo)原點(diǎn)),![]() 的最大值.
的最大值.
【答案】I.![]() ;Ⅱ.2
;Ⅱ.2
【解析】
I:根據(jù)離心率得到![]() ,由三角形面積公式得到
,由三角形面積公式得到![]() ,進(jìn)而求出參數(shù)值,和方程;Ⅱ:當(dāng)AB
,進(jìn)而求出參數(shù)值,和方程;Ⅱ:當(dāng)AB![]() x軸時,
x軸時,![]() ,當(dāng)AB與x軸不垂直時,設(shè)直線AB的方程為
,當(dāng)AB與x軸不垂直時,設(shè)直線AB的方程為![]() ,根據(jù)直線和圓的位置關(guān)系得到
,根據(jù)直線和圓的位置關(guān)系得到![]() ,由
,由![]() =
=![]() ,借助于韋達(dá)定理表示求解即可.
,借助于韋達(dá)定理表示求解即可.
I.由題設(shè):![]()
兩焦點(diǎn)與短軸的一個端點(diǎn)的連線構(gòu)成的三角形面積為![]() ,
,
解得![]()
∴橢圓C的方程為![]()
Ⅱ.設(shè)![]()
1.當(dāng)AB![]() x軸時,
x軸時,![]()
2.當(dāng)AB與x軸不垂直時,設(shè)直線AB的方程為![]()
由已知![]() ,得
,得![]()
設(shè)三角形OAB的高為h即圓的半徑,直線和圓的切點(diǎn)為M點(diǎn),根據(jù)幾何關(guān)系得到:![]() =
=![]() ,
,
把![]() 代入橢圓方程消去y,
代入橢圓方程消去y,
整理得![]() ,
,
有![]()
得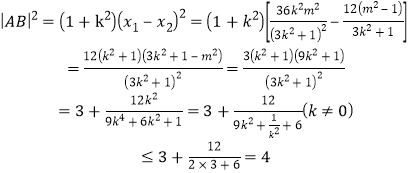
當(dāng)且僅當(dāng)![]() ,即
,即![]() 時等號成立.
時等號成立.
當(dāng)![]() 時,
時,![]()
綜上所述![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
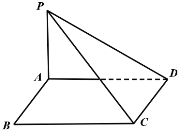
如圖所示的空間幾何體,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角為![]() .且點(diǎn)E在平面ABC上的射影落在
.且點(diǎn)E在平面ABC上的射影落在![]() 的平分線上.
的平分線上.

(1)求證:DE//平面ABC;
(2)求二面角E—BC—A的余弦;
(3)求多面體ABCDE的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓E:![]() 的離心率是
的離心率是![]() ,
,![]() ,
,![]() 分別為橢圓E的左右頂點(diǎn),B為上頂點(diǎn),
分別為橢圓E的左右頂點(diǎn),B為上頂點(diǎn),![]() 的面積為
的面積為![]() 直線l過點(diǎn)
直線l過點(diǎn)![]() 且與橢圓E交于P,Q兩點(diǎn).
且與橢圓E交于P,Q兩點(diǎn).

![]() 求橢圓E的標(biāo)準(zhǔn)方程;
求橢圓E的標(biāo)準(zhǔn)方程;
![]() 求
求![]() 面積的最大值;
面積的最大值;
![]() 設(shè)直線
設(shè)直線![]() 與直線
與直線![]() 交于點(diǎn)N,證明:點(diǎn)N在定直線上,并寫出該直線方程.
交于點(diǎn)N,證明:點(diǎn)N在定直線上,并寫出該直線方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】空氣質(zhì)量按照空氣質(zhì)量指數(shù)大小分為七檔(五級),相對應(yīng)空氣質(zhì)量的七個類別,指數(shù)越大,說明污染的情況越嚴(yán)重,對人體危害越大.
指數(shù) | 級別 | 類別 | 戶外活動建議 |
| Ⅰ | 優(yōu) | 可正常活動 |
| Ⅱ | 良 | |
| Ⅲ | 輕微污染 | 易感人群癥狀有輕度加劇,健康人群出現(xiàn)刺激癥狀,心臟病和呼吸系統(tǒng)疾病患者應(yīng)減少體積消耗和戶外活動. |
| 輕度污染 | ||
| Ⅳ | 中度污染 | 心臟病和肺病患者癥狀顯著加劇,運(yùn)動耐受力降低,健康人群中普遍出現(xiàn)癥狀,老年人和心臟病、肺病患者應(yīng)減少體力活動. |
| 中度重污染 | ||
| Ⅴ | 重污染 | 健康人運(yùn)動耐受力降低,由明顯強(qiáng)烈癥狀,提前出現(xiàn)某些疾病,老年人和病人應(yīng)當(dāng)留在室內(nèi),避免體力消耗,一般人群應(yīng)盡量減少戶外活動. |
現(xiàn)統(tǒng)計(jì)邵陽市市區(qū)2016年1月至11月連續(xù)60天的空氣質(zhì)量指數(shù),制成如圖所示的頻率分布直方圖.
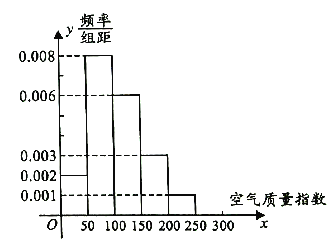
(1)求這60天中屬輕度污染的天數(shù);
(2)求這60天空氣質(zhì)量指數(shù)的平均值;
(3)一般地,當(dāng)空氣質(zhì)量為輕度污染或輕度污染以上時才會出現(xiàn)霧霾天氣,且此時出現(xiàn)霧霾天氣的概率為![]() ,請根據(jù)統(tǒng)計(jì)數(shù)據(jù),求在未來2天里,邵陽市恰有1天出現(xiàn)霧霾天氣的概率.
,請根據(jù)統(tǒng)計(jì)數(shù)據(jù),求在未來2天里,邵陽市恰有1天出現(xiàn)霧霾天氣的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() ,
,![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)若函數(shù)![]() 的圖象在
的圖象在![]() 處的切線與直線
處的切線與直線![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)關(guān)于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范圍;
的取值范圍;
(3)討論函數(shù)![]() 極值點(diǎn)的個數(shù).
極值點(diǎn)的個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,已知在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,且
,且![]() .
.
(1)問當(dāng)實(shí)數(shù)![]() 在什么范圍時,
在什么范圍時,![]() 邊上能存在點(diǎn)
邊上能存在點(diǎn)![]() ,使得
,使得![]() ?
?
(2)當(dāng)![]() 邊上有且僅有一個點(diǎn)
邊上有且僅有一個點(diǎn)![]() 使得
使得![]() 時,求二面角
時,求二面角![]() 的余弦值大小.
的余弦值大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在邊
在邊![]() 上,點(diǎn)
上,點(diǎn)![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點(diǎn)分別為
的對稱點(diǎn)分別為![]() ,則
,則![]() 的面積的最大值為
的面積的最大值為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有下列四個命題:
①“若a2+b2=0,則a,b全為0”的逆否命題是“若a,b全不為0,則a2+b2≠0”
②若事件A與事件B互斥,則P(A∪B)=P(A)+P(B);
③在△ABC中,“A<B”是“sinA<sinB”成立的充要條件;
④若α、β是兩個相交平面,直線mα,則在平面β內(nèi),一定存在與直線m平行的直線.
上述命題中,其中真命題的序號是_____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解某養(yǎng)殖產(chǎn)品在某段時間內(nèi)的生長情況,在該批產(chǎn)品中隨機(jī)抽取了120件樣本,測量其增長長度(單位:![]() ),經(jīng)統(tǒng)計(jì)其增長長度均在區(qū)間
),經(jīng)統(tǒng)計(jì)其增長長度均在區(qū)間![]() 內(nèi),將其按
內(nèi),將其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
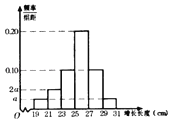
,![]() 分成6組,制成頻率分布直方圖,如圖所示其中增長長度為
分成6組,制成頻率分布直方圖,如圖所示其中增長長度為![]() 及以上的產(chǎn)品為優(yōu)質(zhì)產(chǎn)品.
及以上的產(chǎn)品為優(yōu)質(zhì)產(chǎn)品.
(Ⅰ)求圖中![]() 的值;
的值;
(Ⅱ)已知這120件產(chǎn)品來自于![]() ,
,![]() 兩個試驗(yàn)區(qū),部分?jǐn)?shù)據(jù)如下列聯(lián)表:
兩個試驗(yàn)區(qū),部分?jǐn)?shù)據(jù)如下列聯(lián)表:
|
| 合計(jì) | |
優(yōu)質(zhì)產(chǎn)品 | 20 | ||
非優(yōu)質(zhì)產(chǎn)品 | 60 | ||
合計(jì) |
將聯(lián)表補(bǔ)充完整,并判斷是否有![]() 的把握認(rèn)為優(yōu)質(zhì)產(chǎn)品與
的把握認(rèn)為優(yōu)質(zhì)產(chǎn)品與![]() ,
,![]() 兩個試驗(yàn)區(qū)有關(guān)系,并說明理由;
兩個試驗(yàn)區(qū)有關(guān)系,并說明理由;
下面的臨界值表僅供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,其中
,其中![]() )
)
(Ⅲ)以樣本的頻率代表產(chǎn)品的概率,從這批產(chǎn)品中隨機(jī)抽取4件進(jìn)行分析研究,計(jì)算抽取的這4件產(chǎn)品中含優(yōu)質(zhì)產(chǎn)品的件數(shù)![]() 的分布列和數(shù)學(xué)期望
的分布列和數(shù)學(xué)期望![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com