
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 在邊
在邊![]() 上,點
上,點![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點分別為
的對稱點分別為![]() ,則
,則![]() 的面積的最大值為
的面積的最大值為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
解三角形,建立坐標(biāo)系,設(shè)AD斜率為k,用k表示出B′縱坐標(biāo),代入面積公式得出面積關(guān)于k的函數(shù),根據(jù)k的范圍和函數(shù)單調(diào)性求出面積最大值.
由余弦定理可得AC2=AB2+BC2﹣2ABBCcosB=12+9﹣2×2![]() 3
3![]() 3,
3,
∴AC![]() ,且AC2+BC2=AB2,
,且AC2+BC2=AB2,
∴AC⊥BC,
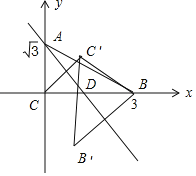
以C為原點,以CB,CA為坐標(biāo)軸建立平面直角坐標(biāo)系,如圖所示:
設(shè)直線AD的方程為y=kx![]() ,
,
當(dāng)D與線段AB的端點重合時,B,B',C'在同一條直線上,不符合題意,
∴則k![]() ,設(shè)B′(m,n),顯然n<0,
,設(shè)B′(m,n),顯然n<0,
則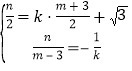 ,解得n
,解得n![]() ,
,
∵CC′∥BB′,
∴S△BB′C′=S△BB′C![]() ,
,
令f(k)![]() (k
(k![]() ),則f′(k)
),則f′(k)![]() ,
,
令f′(k)=0可得k![]() 或k
或k![]() (舍),
(舍),
∴當(dāng)k![]() 時,f′(k)>0,當(dāng)
時,f′(k)>0,當(dāng)![]() k
k![]() 時,f′(k)<0,
時,f′(k)<0,
∴當(dāng)k![]() 時,f(k)取得最大值f(
時,f(k)取得最大值f(![]() )
)![]() .
.
故選:D.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)某農(nóng)產(chǎn)品近幾年的產(chǎn)量統(tǒng)計如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代碼t | 1 | 2 | 3 | 4 | 5 | 6 |
年產(chǎn)量y(萬噸) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根據(jù)表中數(shù)據(jù),建立![]() 關(guān)于的線性回歸方程
關(guān)于的線性回歸方程![]() ;
;
(Ⅱ)根據(jù)線性回歸方程預(yù)測2019年該地區(qū)該農(nóng)產(chǎn)品的年產(chǎn)量.
附:對于一組數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: ,
,![]() .(參考數(shù)據(jù):
.(參考數(shù)據(jù):![]() ,計算結(jié)果保留小數(shù)點后兩位)
,計算結(jié)果保留小數(shù)點后兩位)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,點
,點![]() 在橢圓上,有
在橢圓上,有![]() ,橢圓的離心率為
,橢圓的離心率為![]() ;
;
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)已知![]() ,過點
,過點![]() 作直線
作直線![]() 與橢圓交于
與橢圓交于![]() 不同兩點,線段
不同兩點,線段![]() 的中垂線為
的中垂線為![]() ,線段
,線段![]() 的中點為
的中點為![]() 點,記
點,記![]() 與
與![]() 軸的交點為
軸的交點為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 過點
過點![]() ,且圓心在直線
,且圓心在直線![]() 上.
上.
(1)求圓![]() 的方程;
的方程;
(2)平面上有兩點![]() ,點
,點![]() 是圓
是圓![]() 上的動點,求
上的動點,求![]() 的最小值;
的最小值;
(3)若![]() 是
是![]() 軸上的動點,
軸上的動點,![]() 分別切圓
分別切圓![]() 于
于![]() 兩點,試問:直線
兩點,試問:直線![]() 是否恒過定點?若是,求出定點坐標(biāo),若不是,說明理由.
是否恒過定點?若是,求出定點坐標(biāo),若不是,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)對設(shè)備進行技術(shù)升級改造,為了檢驗改造效果,現(xiàn)從設(shè)備改造后生產(chǎn)的大量產(chǎn)品中抽取了100件產(chǎn)品作為樣本,檢測一項質(zhì)量指標(biāo)值,統(tǒng)計整理為如圖所示的頻率分布直方圖:
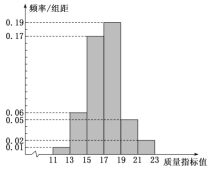
(1)估計該企業(yè)所生產(chǎn)產(chǎn)品的質(zhì)量指標(biāo)的平均數(shù)和中位數(shù)(中位數(shù)保留一位小數(shù));
(2)若產(chǎn)品的質(zhì)量指標(biāo)在![]() 內(nèi),則該產(chǎn)品為殘次品,生產(chǎn)并銷售一件殘次品該企業(yè)損失1萬元;若產(chǎn)品的質(zhì)量指標(biāo)在
內(nèi),則該產(chǎn)品為殘次品,生產(chǎn)并銷售一件殘次品該企業(yè)損失1萬元;若產(chǎn)品的質(zhì)量指標(biāo)在![]() 范圍內(nèi),則該產(chǎn)品為特優(yōu)品,生產(chǎn)一件特優(yōu)品該企業(yè)獲利3萬元.把樣本中的殘次品和特優(yōu)品取出合并在一起,在從中任取2件產(chǎn)品進行銷售,那么該企業(yè)收入為多少萬元的可能性最大?
范圍內(nèi),則該產(chǎn)品為特優(yōu)品,生產(chǎn)一件特優(yōu)品該企業(yè)獲利3萬元.把樣本中的殘次品和特優(yōu)品取出合并在一起,在從中任取2件產(chǎn)品進行銷售,那么該企業(yè)收入為多少萬元的可能性最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 是由兩個全等的菱形
是由兩個全等的菱形![]() 和
和![]() 組成的空間圖形,
組成的空間圖形,![]() ,∠BAF=∠ECD=60°.
,∠BAF=∠ECD=60°.
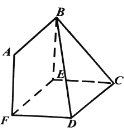
(1)求證:![]() ;
;
(2)如果二面角B-EF-D的平面角為60°,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于無窮數(shù)列{an},記T={x|x=aj﹣ai,i<j},若數(shù)列{an}滿足:“存在t∈T,使得只要am﹣ak=t(m,k∈N*,m>k),必有am+1﹣ak+1=t”,則稱數(shù)列具有性質(zhì)P(t).
(1)若數(shù)列{an}滿足![]() ,判斷數(shù)列{an}是否具有性質(zhì)P(2)?是否具有性質(zhì)P(4)?說明理由;
,判斷數(shù)列{an}是否具有性質(zhì)P(2)?是否具有性質(zhì)P(4)?說明理由;
(2)求證:“T是有限集”是“數(shù)列{an}具有性質(zhì)P(0)”的必要不充分條件;
(3)已知{bn}是各項均為正整數(shù)的數(shù)列,且{bn}既具有性質(zhì)P(2),又具有性質(zhì)P(5),求證:存在正整數(shù)N,使得aN,aN+1,aN+2,…,aN+K,…是等差數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】點![]() 為
為![]() 所在的平面內(nèi),給出下列關(guān)系式:
所在的平面內(nèi),給出下列關(guān)系式:
①![]() ;
;
② ;
;
③![]() .
.
則點![]() 依次為
依次為![]() 的( )
的( )
A.內(nèi)心、重心、垂心B.重心、內(nèi)心、垂心C.重心、內(nèi)心、外心D.外心、垂心、重心
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國是世界上嚴(yán)重缺水的國家,某市為了制定合理的節(jié)水方案,對居民用水情況進行調(diào)查,通過抽樣,獲得某年100為居民每人的月均用水量(單位:噸),將數(shù)據(jù)按照![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
(1)求直方圖的![]() 的值;
的值;
(2)設(shè)該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數(shù),說明理由.
(3)估計居民月用水量的中位數(shù).

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com