
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,且sinA+![]() cosA=2.
cosA=2.
(Ⅰ)求角A的大小;
(Ⅱ)現給出三個條件:①a=2;②B=45°;③c= ![]() .試從中選出兩個可以確△ABC的條件,寫出你的選擇,并以此為依據求△ABC的面積.(只寫出一個方案即可)
.試從中選出兩個可以確△ABC的條件,寫出你的選擇,并以此為依據求△ABC的面積.(只寫出一個方案即可)
【答案】(Ⅰ)![]() (Ⅱ) 選擇①②,
(Ⅱ) 選擇①②, ![]()
【解答】解:(Ⅰ)依題意得2sin(A+![]() )=2,即sin(A+
)=2,即sin(A+![]() )=1,
)=1,
∵0<A<π,
∴![]() <A+
<A+![]() <
<![]() ,
,
∴A+![]() =
=![]() ,
,
∴A=![]() .
.
(Ⅱ)選擇①②由正弦定理![]() =
=![]() ,得b=
,得b=![]() sinB=2
sinB=2![]() ,
,
∵A+B+C=π,
∴sinC=sin(A+B)=sinAcosB+cosAsinB=![]() +
+![]() ,
,
∴S=![]() absinC=
absinC=![]() ×2×2
×2×2![]() ×
×![]() =
=![]() +1.
+1.
【解析】試題分析:(1)根據題目條件,利用輔助角公式,再結合![]() 是三角形的內角,即可求出
是三角形的內角,即可求出![]() 的大小;(2)根據(1)的結論,利用條件①
的大小;(2)根據(1)的結論,利用條件①![]() , ②
, ②![]() ,并結合正弦定理,即可求出
,并結合正弦定理,即可求出![]() 邊,進而可求出
邊,進而可求出![]() 邊和角
邊和角![]() ,從而可確定
,從而可確定![]() ,并可以求得其面積.
,并可以求得其面積.
試題解析:(1)由![]() ,得
,得![]()
因為![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]()
(2)方案一:選①和②
由正弦定理得, ![]()
又, ![]()
![]() 的面積為
的面積為![]()
方案二:選①和③
由余弦定理得, ![]()
則![]() ,
,
解得![]() ,于是
,于是![]()
![]() 的面積為
的面積為![]()


科目:高中數學 來源: 題型:
【題目】某工廠甲、乙兩個車間包裝同一種產品,在自動包裝傳送帶上每隔1小時抽一包產品,稱其重量(單位:克)是否合格,分別做記錄,抽查數據如下:
甲車間:102,101,99,98,103,98,99;
乙車間:110,115,90,85,75,115,110.
(1)問:這種抽樣是何種抽樣方法;
(2)估計甲、乙兩車間包裝產品的質量的均值與方差,并說明哪個均值的代表性好,哪個車間包裝產品的質量較穩定.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解廣告投入對銷售收益的影響,在若干地區各投入4萬元廣告費,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示),由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從0開始計數的. 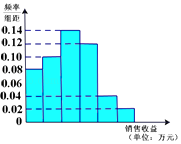
(1)根據頻率分布直方圖計算各小長方形的寬度;
(2)估計該公司投入4萬元廣告費之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值)
(3)該公司按照類似的研究方法,測得另外一些數據,并整理得到下表:
廣告投入x(單位:萬元) | 1 | 2 | 3 | 4 | 5 |
銷售收益y(單位:萬元) | 2 | 3 | 2 | 7 |
表格中的數據顯示,x與y之間存在線性相關關系,請將(2)的結果填入空白欄,并計算y關于x的回歸方程.
回歸直線的斜率和截距的最小二乘法估計公式分別為  ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知長方體ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的點,且BE⊥B1C.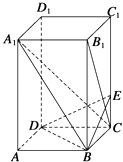
(1)求CE的長;
(2)求證:A1C⊥平面BED;
(3)求A1B與平面BDE夾角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有一塊大型的廣告宣傳版面,其形狀如圖所示的直角梯形![]() .某廠家因產品宣傳的需要,擬出資規劃出一塊區域(圖中陰影部分)為產品做廣告,形狀為直角梯形
.某廠家因產品宣傳的需要,擬出資規劃出一塊區域(圖中陰影部分)為產品做廣告,形狀為直角梯形![]() (點
(點![]() 在曲線段
在曲線段![]() 上,點
上,點![]() 在線段
在線段![]() 上).已知
上).已知![]() ,
,![]() ,其中曲線段
,其中曲線段![]() 是以
是以![]() 為頂點,
為頂點,![]() 為對稱軸的拋物線的一部分.
為對稱軸的拋物線的一部分.

(1)求線段![]() ,線段
,線段![]() ,曲線段
,曲線段![]() 所圍成區域的面積;
所圍成區域的面積;
(2)求廠家廣告區域![]() 的最大面積.
的最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地農業監測部門統計發現:該地區近幾年的生豬收購價格每四個月會重復出現,但生豬養殖成本逐月遞增.下表是今年前四個月的統計情況:
月份 | 1月份 | 2月份 | 3月份 | 4月份 |
收購價格(元/斤) | 6 | 7 | 6 | 5 |
養殖成本(元/斤) | 3 | 4 | 4.6 | 5 |
現打算從以下兩個函數模型:
①y=Asin(ωx+φ)+B,(A>0,ω>0,﹣π<φ<π),
②y=log2(x+a)+b
中選擇適當的函數模型,分別來擬合今年生豬收購價格(元/斤)與相應月份之間的函數關系、養殖成本(元/斤)與相應月份之間的函數關系.
(1)請你選擇適當的函數模型,分別求出這兩個函數解析式;
(2)按照你選定的函數模型,幫助該部門分析一下,今年該地區生豬養殖戶在8月和9月有沒有可能虧損?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com