
���}Ŀ����D��O������(bi��o)ԭ�c(di��n)���c(di��n)F�钁�タC1��![]() �Ľ��c(di��n)���Ғ��タC1���c(di��n)P̎���о��c�AC2��
�Ľ��c(di��n)���Ғ��タC1���c(di��n)P̎���о��c�AC2��![]() �������c(di��n)Q��
�������c(di��n)Q��

��������(d��ng)ֱ��PQ�ķ��̞�![]() �r(sh��)���� ���タC1�ķ��̣�
�r(sh��)���� ���タC1�ķ��̣�
��������(d��ng)����(sh��)P׃���r(sh��)��ӛS1 ��S2�քe���FPQ����FOQ����e����![]() ����Сֵ��
����Сֵ��
���𰸡���1��x2=4![]() y����2��
y����2��![]() .
.
��������
ԇ�}�������������O(sh��)�c(di��n)P��x0��![]() ������x2=2py��p��0���ã�y=
������x2=2py��p��0���ã�y=![]() ����(d��o)y��=
����(d��o)y��=![]() ��
��
��?y��n)�ֱ��PQ��б�ʞ�1������![]() =1��x0 -
=1��x0 -![]() -��2=0�����p=2
-��2=0�����p=2![]() ��
��
���Ԓ��タC1 �ķ��̞�x2=4![]() y��
y��
��������?y��n)��c(di��n)P̎���о����̞飺y-![]() =
=![]() ��x-x0������2x0x-2py-x02=0��
��x-x0������2x0x-2py-x02=0��
�� OQ�ķ��̞�y=-![]() x
x
����(j��)��c�A����d=r����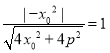 ������(ji��n)��x04=4x02+4p2��
������(ji��n)��x04=4x02+4p2��
�ɷ��̽M �����Q��
�����Q��![]() ��
��![]() ����
����
����|PQ|=��1+k2|xP-xQ|=
�c(di��n)F��0��![]() �����о�PQ�ľ��x��d=
�����о�PQ�ľ��x��d= ��
��
����S1=
![]() =
=![]() ��
��
S2=![]() ��
��
����x04=4x02+4p2֪��4p2=x04-4x02��0����|x0|��2��
����![]()
=![]()
=![]() +3��2
+3��2![]() +3����(d��ng)�҃H��(d��ng)
+3����(d��ng)�҃H��(d��ng)![]() �r(sh��)ȡ��=��̖(h��o)��
�r(sh��)ȡ��=��̖(h��o)��
��x02=4+2![]() ���˕r(sh��)��p=
���˕r(sh��)��p=![]() ��
��
����![]() ����Сֵ��2
����Сֵ��2![]() +3��
+3��


 ���(zh��n)�п�����ϵ�д�
���(zh��n)�п�����ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�� ��һ��(g��)�ض��r(sh��)��(n��i)�����c(di��n)E�����ĵ�7�����ԃ�(n��i)�����O(sh��)�龯��ˮ��.�c(di��n)E����55����̎��һ��(g��)���_(d��)�^�y(c��)վA.ij�r(sh��)�̜y(c��)��һ�҄���ֱ�����Ĵ�ֻλ���c(di��n)A��ƫ�|![]() ���c�c(di��n)A���40
���c�c(di��n)A���40![]() �����λ��B����(j��ng)�^(gu��)40����֜y(c��)��ԓ�������c(di��n)A��ƫ�|
�����λ��B����(j��ng)�^(gu��)40����֜y(c��)��ԓ�������c(di��n)A��ƫ�|![]() +
+![]() (����sin
(����sin![]() =
=![]() ��
��![]() )���c�c(di��n)A���10
)���c�c(di��n)A���10![]() ������C.
������C.
��I����ԓ��������ٶȣ���λ������/С�r(sh��)��;
��II����ԓ������׃���з����^�m(x��)���.�Д����Ƿ��(hu��)�M(j��n)�뾯��ˮ���f(shu��)������.


�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() �锵(sh��)��
�锵(sh��)��![]() ��ǰ�(xi��ng)�ͣ�
��ǰ�(xi��ng)�ͣ�![]() ��
��![]() ��
��![]() �c
�c![]() �ĵȱ����(xi��ng).
�ĵȱ����(xi��ng).
��1����(sh��)��![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
��2����![]() ������(sh��)��
������(sh��)��![]() ����(sh��)��
����(sh��)��![]() ��ǰ
��ǰ![]() �(xi��ng)��
�(xi��ng)��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���o�����нY(ji��)Փ��
��(d��ng)�c(di��n)![]() �քe���ɶ��c(di��n)��-3,0������3,0�� �B����б��֮�˷e��
�քe���ɶ��c(di��n)��-3,0������3,0�� �B����б��֮�˷e��![]() ���O(sh��)
���O(sh��)![]() ��܉�E������
��܉�E������![]() ���քe������
���քe������![]() �����ҽ��c(di��n)���t�����f(shu��)���У�
�����ҽ��c(di��n)���t�����f(shu��)���У�
��1������![]() �Ľ��c(di��n)����(bi��o)��
�Ľ��c(di��n)����(bi��o)��![]() ��
��
��2����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() �ă�(n��i)�ЈA�A����ֱ��
�ă�(n��i)�ЈA�A����ֱ��![]() �ϣ�
�ϣ�
��3����![]() ���t
���t![]() ��
��
��4���O(sh��)![]() ���t
���t![]() ����Сֵ��
����Сֵ��![]() ��
��
�������_����̖(h��o)�ǣ�_____________��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����֪���タ![]() ��
��![]() ���^(gu��)���c(di��n)
���^(gu��)���c(di��n)![]() б�ʴ������ֱ��
б�ʴ������ֱ��![]() �����タ��
�����タ��![]() ��
��![]() ���c(di��n)�����c���(zh��n)�������c(di��n)
���c(di��n)�����c���(zh��n)�������c(di��n)![]() ��
��
��1��������![]() ���L(zh��ng)��
���L(zh��ng)��![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
��2����![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ�Ì�(du��)����ֱ��
��ʹ�Ì�(du��)����ֱ��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ��б��ʼ�K�ɵȲ(sh��)�У����������c(di��n)
��б��ʼ�K�ɵȲ(sh��)�У����������c(di��n)![]() ������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
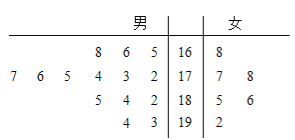
���}Ŀ��![]() ��˾��ij��W(xu��)���ծ��I(y��)������(j��ng)�^(gu��)�C�Ϝy(c��)ԇ�������14��������6��Ů�����@20�����I(y��)���Ĝy(c��)ԇ�ɿ�(j��)?n��i)��o�~�D��ʾ����λ���֣�����˾Ҏ(gu��)�����ɿ�(j��)?c��)?80�������ߵ����ײ��T��������180�������ߵ����Ҳ��T��������
��˾��ij��W(xu��)���ծ��I(y��)������(j��ng)�^(gu��)�C�Ϝy(c��)ԇ�������14��������6��Ů�����@20�����I(y��)���Ĝy(c��)ԇ�ɿ�(j��)?n��i)��o�~�D��ʾ����λ���֣�����˾Ҏ(gu��)�����ɿ�(j��)?c��)?80�������ߵ����ײ��T��������180�������ߵ����Ҳ��T��������
��1���������ɿ�(j��)����λ��(sh��)��Ů���ɿ�(j��)��ƽ��ֵ��
��2������÷ӳ�ӵķ��������ײ��T�����x�����Ҳ��T�����x�й��xȡ5�ˣ���?g��u)��@5�����x2�ˣ���ô������һ�������ײ��T�����x�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��(j��)![]() ��
��![]() ��
��![]() ������
������![]() �Ǘ���(qi��ng)�h��ͨ��
�Ǘ���(qi��ng)�h��ͨ��![]() ��
��![]() ��
��![]() ����(g��)�˵������룬�O(sh��)
����(g��)�˵������룬�O(sh��)![]() ��(g��)��(sh��)��(j��)����λ��(sh��)��
��(g��)��(sh��)��(j��)����λ��(sh��)��![]() ��ƽ����(sh��)��
��ƽ����(sh��)��![]() �������
�������![]() ������ټ�����������������
������ټ�����������������![]() ���t�@
���t�@![]() ��(g��)��(sh��)��(j��)���������f(shu��)�����_������ ��
��(g��)��(sh��)��(j��)���������f(shu��)�����_������ ��
A��������ƽ����(sh��)������ӣ���λ��(sh��)һ��׃������ܲ�׃
B��������ƽ����(sh��)������ӣ���λ��(sh��)���ܲ�׃������׃��
C��������ƽ����(sh��)������ӣ���λ��(sh��)���ܲ�׃������Ҳ��׃
D��������ƽ����(sh��)���ܲ�׃����λ��(sh��)���ܲ�׃��������ܲ�׃
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() �����䌧(d��o)����(sh��)��
�����䌧(d��o)����(sh��)��![]() ��
��
��1����(sh��)![]() �ĘOֵ��
�ĘOֵ��
��2����(d��ng)![]() �r(sh��)���P(gu��n)��
�r(sh��)���P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() ���������
���������![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����������![]() �У�����
�У�����![]() �����Σ���
��������![]() .
.
��1�� ���C: ƽ��![]() ƽ��
ƽ�� ![]() ;
;
��2����![]() ,��ƽ��
,��ƽ��![]() �cƽ��
�cƽ��![]() ���ɽǵĴ�С.
���ɽǵĴ�С.

�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com