
已知函數 .
.
(1)求證: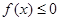 ;
;
(2)若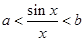 對
對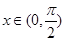 恒成立,求
恒成立,求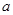 的最大值與
的最大值與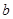 的最小值.
的最小值.
(1)詳見解析;(2)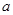 的最大值為
的最大值為 ,
,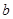 的最小值為1.
的最小值為1.
解析試題分析:(1)求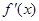 ,由
,由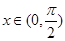 ,判斷出
,判斷出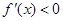 ,得出函數
,得出函數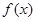 在
在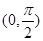 上單調遞減,從而
上單調遞減,從而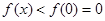 ;(2)由于
;(2)由于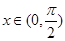 ,“
,“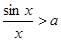 ”等價于“
”等價于“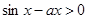 ”,“
”,“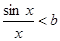 ”等價于“
”等價于“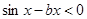 ”,令
”,令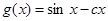 ,則
,則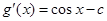 ,對
,對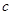 分
分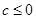 ;
;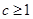 ;
;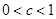 進行討論,
進行討論,
用導數法判斷函數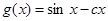 的單調性,從而確定當
的單調性,從而確定當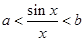 對
對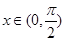 恒成立時
恒成立時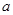 的最大值與
的最大值與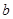 的最小值.
的最小值.
(1)由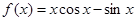 得
得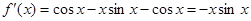 ,
,
因為在區間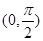 上
上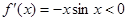 ,所以,
,所以,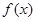 在區間
在區間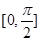 上單調遞減,
上單調遞減,
從而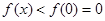 .
.
(2)當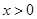 時,“
時,“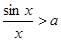 ”等價于“
”等價于“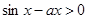 ”,“
”,“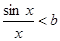 ”等價于“
”等價于“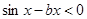 ”,
”,
令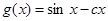 ,則
,則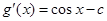 ,
,
當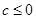 時,
時, 對任意
對任意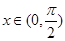 恒成立,
恒成立,
當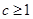 時,因為對任意
時,因為對任意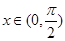 ,
,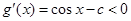 ,所以
,所以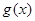 在區間
在區間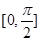 上單調遞減,從而
上單調遞減,從而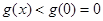 對任意
對任意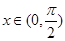 恒成立.
恒成立.
當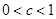 時 ,存在唯一的
時 ,存在唯一的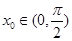 使得
使得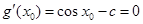 ,
,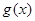 、
、 在區間
在區間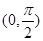 上的情況如下表:
上的情況如下表: