
【題目】某醫藥研究所開發一種新藥,在試驗藥效時發現:如果成人按規定劑量服用,那么服藥后每毫升血液中的含藥量y(微克)與時間x(小時)之間滿足y= 其對應曲線(如圖所示)過點
其對應曲線(如圖所示)過點![]() .
.

(1)試求藥量峰值(y的最大值)與達峰時間(y取最大值時對應的x值);
(2)如果每毫升血液中含藥量不少于1微克時治療疾病有效,那么成人按規定劑量服用該藥后一次能維持多長的有效時間(精確到0.01小時)?
【答案】(1)y取最大值時,對應的x值為1.(2)3.85小時
【解析】(1)由曲線過點![]() ,可得
,可得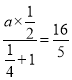 ,故a=8.
,故a=8.
當0<x<1時,y=![]() =4,
=4,
當x≥1時,設2x-1=t,可知t≥1,
y=![]() ≤
≤![]() =4(當且僅當t=1,即x=1時,等號成立).
=4(當且僅當t=1,即x=1時,等號成立).
綜上可知ymax=4,且當y取最大值時,對應的x值為1.
所以藥量峰值為4微克,達峰時間為1小時.
(2)當0<x<1時,由![]() =1,可得x2-8x+1=0,
=1,可得x2-8x+1=0,
解得x=4±![]() ,又4+
,又4+![]() >1,故x=4-
>1,故x=4-![]() .
.
當x≥1時,設2x-1=t,則t≥1,![]() =1,可得
=1,可得![]() =1,解得t=4±
=1,解得t=4±![]() ,
,
又t≥1,故t=4+![]() ,所以2x-1=4+
,所以2x-1=4+![]() ,可得x=log2(4+
,可得x=log2(4+![]() )+1.
)+1.
由圖像知當y≥1時,對應的x的取值范圍是[4-![]() ,log2(4+
,log2(4+![]() )+1],
)+1],
log2(4+![]() )+1-(4-
)+1-(4-![]() )≈3.85,
)≈3.85,
所以成人按規定劑量服用該藥后一次能維持大約3.85小時的有效時間.


 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:
【題目】某種產品的廣告費支出![]() 與銷售額
與銷售額![]() (單位:萬元)之間有如下對應數據:
(單位:萬元)之間有如下對應數據:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求回歸直線方程;
(2)試預測廣告費支出為![]() 萬元時,銷售額多大?
萬元時,銷售額多大?
(3)在已有的五組數據中任意抽取兩組,求至少有一組數據其預測值與實際值之差的絕對值不超過![]() 的概率.(參考數據:
的概率.(參考數據: 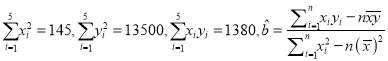 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業接到生產3000臺某產品的A,B,C三種部件的訂單,每臺產品需要這三種部件的數量分別為2,2,1(單位:件).已知每個工人每天可生產A部件6件,或B部件3件,或C部件2件.該企業計劃安排200名工人分成三組分別生產這三種部件,生產B部件的人數與生產A部件的人數成正比,比例系數為k(k為正整數).
(1)設生產A部件的人數為x,分別寫出完成A,B,C三種部件生產需要的時間;
(2)假設這三種部件的生產同時開工,試確定正整數k的值,使完成訂單任務的時間最短,并給出時間最短時具體的人數分組方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一鮮花店一個月(30天)某種鮮花的日銷售量與銷售天數統計如下:
日銷售量(枝) | 0~49 | 50~99 | 100~149 | 150~199 | 200~250 |
銷售天數(天) | 3天 | 3天 | 15天 | 6天 | 3天 |
將日銷售量落入各組區間的頻率視為概率.
(1)試求這30天中日銷售量低于100枝的概率;
(2)若此花店在日銷售量低于100枝的6天中選擇2天作促銷活動,求這2天的日銷售量都低于50枝的概率(不需要枚舉基本事件).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:
①分類變量![]() 與
與![]() 的隨機變量
的隨機變量![]() 越大,說明“
越大,說明“![]() 與
與![]() 有關系”的可信度越大.
有關系”的可信度越大.
②以模型![]() 去擬合一組數據時,為了求出回歸方程,設
去擬合一組數據時,為了求出回歸方程,設![]() ,將其變換后得到線性方程
,將其變換后得到線性方程![]() ,則
,則![]() 的值分別是
的值分別是![]() 和0.3.
和0.3.
③根據具有線性相關關系的兩個變量的統計數據所得的回歸直線方程為![]() 中,
中, ![]() ,
,
則![]() .正確的個數是( )
.正確的個數是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|2-a≤x≤2+a},B={x|x≤1或x≥4}.
(1)當a=3時,求A∩B;
(2)若a>0,且A∩B=![]() ,求實數a的取值范圍.
,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com