
【題目】在甲、乙兩個盒子中分別裝有編號為1,2,3,4的四個形狀相同的小球,現從甲、乙兩個盒子中各取出2個小球,每個小球被取出的可能性相等.
(1)求從甲盒中取出的兩個球上的編號不都是奇數的概率;
(2)求從甲盒取出的小球上編號之和與從乙盒中取出的小球上編號之和相等的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)任取2球的基本事件總數為6,用列舉法列出事件“從甲盒中取出的兩個球上的編號不都是奇數”所含的基本事件,計數后可得概率;
(2)由(1)知從甲,乙兩個盒子中各取2個小球的基本事件總數為![]() 36,用列舉法列出事件“從甲盒取出的小球上編號之和與從乙盒中取出的小球上編號之和相等”所含有的基本事件,計數后可計算概率.
36,用列舉法列出事件“從甲盒取出的小球上編號之和與從乙盒中取出的小球上編號之和相等”所含有的基本事件,計數后可計算概率.
解:(1)記“從甲盒中取出的兩個球上的編號不都是奇數”為事件A,由題意可知,從甲盒中取2個小球的基本事件總數為6,則事件A的基本事件有:
(1,2),(1,4),(2,3),(2,4),(3,4),共5個.∴P(A)=![]() .
.
(2)由題意可知,記“從甲盒取出的小球上編號之和與從乙盒中取出的小球上編號之和相等”為事件B,由題意可知,從甲,乙兩個盒子中各取2個小球的基本事件總數為36,則事件B包含:(12,12),(13,13),(14,14),(14,23),(23,14),(23,23),(24,24),(34,34),共8個基本事件.∴P(B)=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,則稱
成立,則稱![]() 為
為![]() 的不動點,已知函數
的不動點,已知函數![]()
(1)當![]() ,
,![]() 時,求函數
時,求函數![]() 的不動點;
的不動點;
(2)若對任意實數![]() ,函數
,函數![]() 恒有不動點,求
恒有不動點,求![]() 的取值范圍;
的取值范圍;
(3)在(2)條件下,若![]() 圖象上的
圖象上的![]() 兩點的橫坐標是函數
兩點的橫坐標是函數![]() 的不動點,且
的不動點,且![]() 的中點在直線
的中點在直線![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖![]() ,在矩形
,在矩形![]() 中,
中, ![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 為
為![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如圖
(如圖![]() ).
).


圖1 圖2
(Ⅰ)求證: ![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn,對任意的正整數n,都有Sn=![]() an+n-3成立.
an+n-3成立.
(1)求證:存在實數λ使得數列{an+λ}為等比數列;
(2)求數列{nan}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“冰桶挑戰賽”是一項社交網絡上發起的慈善公益活動,活動規定:被邀請者要么在![]() 小時內接受挑戰,要么選擇為慈善機構捐款(不接受挑戰),并且不能重復參加該活動.若被邀請者接受挑戰,則他需在網絡上發布自己被冰水澆遍全身的視頻內容,然后便可以邀請另外
小時內接受挑戰,要么選擇為慈善機構捐款(不接受挑戰),并且不能重復參加該活動.若被邀請者接受挑戰,則他需在網絡上發布自己被冰水澆遍全身的視頻內容,然后便可以邀請另外![]() 個人參與這項活動.假設每個人接受挑戰與不接受挑戰是等可能的,且互不影響.
個人參與這項活動.假設每個人接受挑戰與不接受挑戰是等可能的,且互不影響.
(1)若某參與者接受挑戰后,對其他![]() 個人發出邀請,則這
個人發出邀請,則這![]() 個人中至少有
個人中至少有![]() 個人接受挑戰的概率是多少?
個人接受挑戰的概率是多少?
(2)為了解冰桶挑戰賽與受邀者的性別是否有關,某調查機構進行了隨機抽樣調查,調查得到如下列聯表:
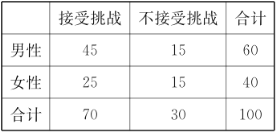
根據表中數據,能否有![]() %的把握認為“冰桶挑戰賽與受邀者的性別有關”?
%的把握認為“冰桶挑戰賽與受邀者的性別有關”?
附: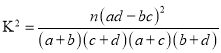

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=![]() ,an+1=3an-1(n∈N*).
,an+1=3an-1(n∈N*).
(1)若數列{bn}滿足bn=an-![]() ,求證:{bn}是等比數列;
,求證:{bn}是等比數列;
(2)求數列{an}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年10月,舉世矚目的中國共產黨第十九次全國代表大會在北京順利召開.某高中為此組織全校2000名學生進行了一次“十九大知識知多少”的問卷測試(滿分:100分),并從中抽取了40名學生的測試成績,得到了如圖所示的頻率分布直方圖.

(1)求圖中實數![]() 的值及樣本中40名學生測試成績的平均數和中位數(同一組中的數據用該組區間的中點值作代表);
的值及樣本中40名學生測試成績的平均數和中位數(同一組中的數據用該組區間的中點值作代表);
(2)(i)利用分層抽樣的方法從成績低于70分的三組學生中抽取7人,再從這7人中隨機抽取2人分析成績不理想的原因,求前2組中至少有1人被抽到的概率;
(2)以頻率估計概率,試估計該校這次測試成績不低于80分的學生人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com