
【題目】已知如圖,橢圓![]() :
:![]() 與直線
與直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點.
兩點.

(Ⅰ)若直線![]() 經過橢圓
經過橢圓![]() 的左焦點
的左焦點![]() ,交
,交![]() 軸于點
軸于點![]() ,且滿足
,且滿足![]() ,
,![]() .求證:
.求證:![]() 為定值;
為定值;
(Ⅱ)若![]() ,求
,求![]() 面積的取值范圍.
面積的取值范圍.
【答案】(Ⅰ)見解析; (Ⅱ)![]() .
.
【解析】
(Ⅰ)設出直線方程,設出AB的坐標,直線方程代入橢圓方程,利用韋達定理結合![]() ,
,![]() .即可證明:λ+μ為定值;(Ⅱ)當直線OA,OB分別與坐標軸重合時,易知
.即可證明:λ+μ為定值;(Ⅱ)當直線OA,OB分別與坐標軸重合時,易知![]() .當直線OA,OB斜率存在且不為0時,設
.當直線OA,OB斜率存在且不為0時,設![]() ,設
,設![]() ,
,![]() ,直線y=kx代入橢圓C得到x2+2k2x2﹣2=0,求出A,B坐標,表示出三角形的面積,利用換元法轉化為二次函數求解三角形的面積的范圍.
,直線y=kx代入橢圓C得到x2+2k2x2﹣2=0,求出A,B坐標,表示出三角形的面積,利用換元法轉化為二次函數求解三角形的面積的范圍.
(Ⅰ)證明:由題設知直線![]() 斜率存在,設直線
斜率存在,設直線![]() 方程為
方程為![]() ,則
,則![]() .
.
設![]() ,
,![]() ,直線
,直線![]() 代入橢圓
代入橢圓![]() 得
得![]() ,
,
所以![]() ,
,![]() ,
,
由![]() ,
,![]() 知
知![]() ,
,![]() ,
,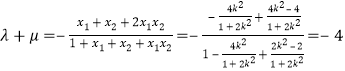 .
.
(Ⅱ)當直線![]() ,
,![]() 分別與坐標軸重合時,易知
分別與坐標軸重合時,易知![]() .
.
當直線![]() ,
,![]() 斜率存在且不為0時,設
斜率存在且不為0時,設![]() :
:![]() ,
,![]() :
:![]() ,
,
設![]() ,
,![]() ,直線
,直線![]() 代入橢圓
代入橢圓![]() 得到
得到![]() ,
,
所以![]() ,
,![]() ,
,
同理![]() ,
,![]() ,
,
![]()
![]() ,
,
令![]() ,
,
則![]()
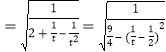 ,
,
因為![]() ,所以
,所以![]() ,
,
故![]() ,綜上
,綜上![]() .
.


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩城相距100![]() ,在兩城之間距甲城
,在兩城之間距甲城![]()
![]() 處的丙地建一核電站給甲、乙兩城供電,為保證城市安全,核電站距兩地的距離不少于10
處的丙地建一核電站給甲、乙兩城供電,為保證城市安全,核電站距兩地的距離不少于10![]() .已知各城供電費用(元)與供電距離(
.已知各城供電費用(元)與供電距離(![]() )的平方和供電量(億千瓦時)之積都成正比,比例系數均是
)的平方和供電量(億千瓦時)之積都成正比,比例系數均是![]() =0.25,若甲城供電量為20億千瓦時/月,乙城供電量為10億千瓦時/月,
=0.25,若甲城供電量為20億千瓦時/月,乙城供電量為10億千瓦時/月,
(1)把月供電總費用![]() (元)表示成
(元)表示成![]() (
(![]() )的函數,并求其定義域;
)的函數,并求其定義域;
(2)求核電站建在距甲城多遠處,才能使月供電總費用最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人在塔的正東方向沿著南偏西60°的方向前進40 m以后,望見塔在東北方向上,若沿途測得塔的最大仰角為30°,則塔高為________________m.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() ,
, ![]() 是橢圓
是橢圓![]() 的左右焦點,
的左右焦點, ![]() 為橢圓
為橢圓![]() 的上頂點,點
的上頂點,點![]() 在橢圓
在橢圓![]() 上,直線
上,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,
, ![]() 為坐標原點,且
為坐標原點,且![]() ,
, ![]() .
.
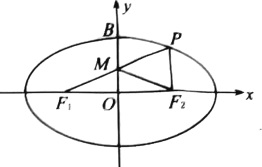
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作兩條互相垂直的直線分別與橢圓
作兩條互相垂直的直線分別與橢圓![]() 交于
交于![]() ,
, ![]() 兩點(異于點
兩點(異于點![]() ),證明:直線
),證明:直線![]() 過定點,并求該定點的坐標.
過定點,并求該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市A,B,C,D四所中學報名參加某高校2015年自主招生考試的學生人數如下表所示:
中學 | A | B | C | D |
人數 | 40 | 30 | 10 | 20 |
該市教委為了解參加考試的學生的學習狀況,采用分層抽樣的方法從四所中學報名參加考試的學生中隨機抽取50名參加問卷調查.則A,B,C,D四所中學抽取的學生人數分別為( )
A.15,20,10,5B.15,20,5,10
C.20,15,10,5D.20,15,5,10
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在甲、乙兩個盒子中分別裝有編號為1,2,3,4的四個形狀相同的小球,現從甲、乙兩個盒子中各取出2個小球,每個小球被取出的可能性相等.
(1)求從甲盒中取出的兩個球上的編號不都是奇數的概率;
(2)求從甲盒取出的小球上編號之和與從乙盒中取出的小球上編號之和相等的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網站舉行“衛生防疫”的知識競賽網上答題,共有120000人通過該網站參加了這次競賽,為了解競賽成績情況,從中抽取了100人的成績進行統計,其中成績分組區間為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其頻率分布直方圖如圖所示,請你解答下列問題:
,其頻率分布直方圖如圖所示,請你解答下列問題:
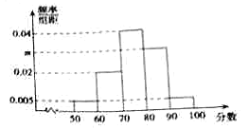
(1)求![]() 的值;
的值;
(2)成績不低于90分的人就能獲得積分獎勵,求所有參賽者中獲得獎勵的人數;
(3)根據頻率分布直方圖,估計這次知識競賽成績的平均分(用組中值代替各組數據的平均值).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某海濱城市附近海面有一臺風,據監測,當前臺風中心位于城市![]() (如圖)的東偏南
(如圖)的東偏南![]() 方向300千米的海面
方向300千米的海面![]() 處,并以20千米/時的速度向西偏北45°方向移動,臺風侵襲的范圍為圓形區域,當前半徑為60千米,并以10千米/時的速度不斷增大,問幾個小時后該城市開始受到臺風的侵襲?受到臺風的侵襲的時間有多少小時?
處,并以20千米/時的速度向西偏北45°方向移動,臺風侵襲的范圍為圓形區域,當前半徑為60千米,并以10千米/時的速度不斷增大,問幾個小時后該城市開始受到臺風的侵襲?受到臺風的侵襲的時間有多少小時?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com