【題目】已知關于x的不等式（kx﹣k2﹣4）（x﹣4）＞0，其中k∈R；
（1）當k=4時，求上述不等式的解集；
（2）當上述不等式的解集為（﹣5，4）時，求k的值．
【答案】
（1）解：關于x的不等式（kx﹣k2﹣4）（x﹣4）＞0，
當k=4時，不等式化為（4x﹣16﹣4）（x﹣4）＞0，
解得x＜4或x＞5，
所以不等式的解集為（﹣∞，4）∪（5，+∞）；
（2）解：當不等式（kx﹣k2﹣4）（x﹣4）＞0的解集為（﹣5，4）時，
有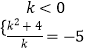 
，
解得k=﹣1或k=﹣4．
【解析】（1）當k=4時，不等式化為（4x﹣16﹣4）（x﹣4）＞0，求出解集即可，（2）不等式的解集為（﹣5，4）時，可得出一根為4，一根為-5，即可解得k的大小.
【考點精析】利用解一元二次不等式對題目進行判斷即可得到答案，需要熟知求一元二次不等式
解集的步驟：一化：化二次項前的系數為正數;二判：判斷對應方程的根;三求：求對應方程的根;四畫：畫出對應函數的圖象;五解集：根據圖象寫出不等式的解集;規律：當二次項系數為正時，小于取中間，大于取兩邊．
狀元坊全程突破導練測系列答案科目：高中數學 來源： 題型：
【題目】設函數f（x）=ln（1﹣x）﹣ln（1+x），則f（x）是（ ）
A.奇函數，且在（0，1）上是增函數
B.奇函數，且在（0，1）上是減函數
C.偶函數，且在（0，1）上是增函數
D.偶函數，且在（0，1）上是減函數
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某化工廠生產某種產品，當年產量在150噸至250噸時，每年的生產成本y萬元與年產量x噸之間的關系可可近似地表示為y= 
﹣30x+4000．
（1）若每年的生產總成本不超過2000萬元，求年產量x的取值范圍；
（2）求年產量為多少噸時，每噸的平均成本最低，并求每噸的最低成本．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在長方體ABCD﹣A1B1C1D1中，AD=AA1=1，AB=2，點E在棱AB上移動． 
（1）證明：D1E⊥A1D；
（2）當E為AB的中點時，求點E到面ACD1的距離；
（3）AE等于何值時，二面角D1﹣EC﹣D的大小為 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】非空集合G關于運算⊕滿足：
⑴對任意a，b∈G，都有a+b∈G；
⑵存在e∈G使得對于一切a∈G都有a⊕e=e⊕a=a，
則稱G是關于運算⊕的融洽集，
現有下列集合與運算：
①G是非負整數集，⊕：實數的加法；
②G是偶數集，⊕：實數的乘法；
③G是所有二次三項式構成的集合，⊕：多項式的乘法；
④G={x|x=a+b 
，a，b∈Q}，⊕：實數的乘法；
其中屬于融洽集的是（請填寫編號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在邊長是2的正方體ABCD﹣A1B1C1D1中，E，F分別為AB，A1C的中點．應用空間向量方法求解下列問題． 
（1）求EF的長
（2）證明：EF∥平面AA1D1D；
（3）證明：EF⊥平面A1CD．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
