
【題目】已知函數(shù)![]() (其中
(其中![]()
![]()
![]() ,
,![]() 為自然對(duì)數(shù)的底數(shù)).
為自然對(duì)數(shù)的底數(shù)).
(Ⅰ)若函數(shù)![]() 無極值,求實(shí)數(shù)
無極值,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)當(dāng)![]() 時(shí),證明:
時(shí),證明:![]() .
.
【答案】(1)實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() ;(2)見解析.
;(2)見解析.
【解析】分析:(1)因?yàn)楹瘮?shù)![]() 無極值,所以
無極值,所以![]() 在
在![]() 上單調(diào)遞增或單調(diào)遞減.即
上單調(diào)遞增或單調(diào)遞減.即![]() 或
或![]() 在
在![]() 時(shí)恒成立,求導(dǎo)分析整理即可得到答案;
時(shí)恒成立,求導(dǎo)分析整理即可得到答案;
(2)由(Ⅰ)可知,當(dāng)![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() .欲證
.欲證![]()
![]()
![]() ,只需證
,只需證![]() 即可,構(gòu)造函數(shù)
即可,構(gòu)造函數(shù)![]() =
=![]()
![]()
![]() (
(![]() ),求導(dǎo)分析整理即可.
),求導(dǎo)分析整理即可.
詳解:(Ⅰ)![]() 函數(shù)
函數(shù)![]() 無極值,
無極值,![]()
![]() 在
在![]() 上單調(diào)遞增或單調(diào)遞減.
上單調(diào)遞增或單調(diào)遞減.
即![]() 或
或![]() 在
在![]() 時(shí)恒成立;
時(shí)恒成立;
又![]() ,
,
令![]() ,則
,則![]() ;
;
所以![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增;
上單調(diào)遞增;
![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() ,
,
當(dāng)![]() 時(shí),顯然不成立;
時(shí),顯然不成立;
所以實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.
(Ⅱ)由(Ⅰ)可知,當(dāng)![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() .
.
欲證![]()
![]()
![]() ,只需證
,只需證![]() 即可.
即可.
構(gòu)造函數(shù)![]() =
=![]()
![]()
![]() (
(![]() ),
),
則![]() 恒成立,故
恒成立,故![]() 在
在![]() 單調(diào)遞增,
單調(diào)遞增,
從而![]() .即
.即![]() ,亦即
,亦即![]() .
.
得證![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖![]() ,在梯形
,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 是
是![]() 與
與![]() 的交點(diǎn),將
的交點(diǎn),將![]() 沿
沿![]() 翻折到圖
翻折到圖![]() 中
中![]() 的位置,得到四棱錐
的位置,得到四棱錐![]() .
.
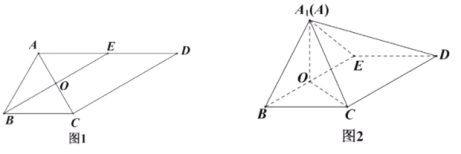
(1)求證:![]() ;
;
(2)當(dāng)![]() ,
,![]() 時(shí),求
時(shí),求![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,點(diǎn)
,點(diǎn)![]() 在棱
在棱![]() 上.
上.
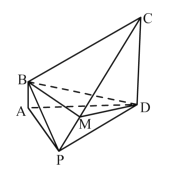
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 平面
平面![]() ,求此時(shí)直線
,求此時(shí)直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】春節(jié)期間某商店出售某種海鮮禮盒,假設(shè)每天該禮盒的需求量在![]() 范圍內(nèi)等可能取值,該禮盒的進(jìn)貨量也在
范圍內(nèi)等可能取值,該禮盒的進(jìn)貨量也在![]() 范圍內(nèi)取值(每天進(jìn)1次貨).商店每銷售1盒禮盒可獲利50元;若供大于求,剩余的削價(jià)處理,每處理1盒禮盒虧損10元;若供不應(yīng)求,可從其它商店調(diào)撥,銷售1盒禮盒可獲利30元.設(shè)該禮盒每天的需求量為
范圍內(nèi)取值(每天進(jìn)1次貨).商店每銷售1盒禮盒可獲利50元;若供大于求,剩余的削價(jià)處理,每處理1盒禮盒虧損10元;若供不應(yīng)求,可從其它商店調(diào)撥,銷售1盒禮盒可獲利30元.設(shè)該禮盒每天的需求量為![]() 盒,進(jìn)貨量為
盒,進(jìn)貨量為![]() 盒,商店的日利潤為
盒,商店的日利潤為![]() 元.
元.
(1)求商店的日利潤![]() 關(guān)于需求量
關(guān)于需求量![]() 的函數(shù)表達(dá)式;
的函數(shù)表達(dá)式;
(2)試計(jì)算進(jìn)貨量![]() 為多少時(shí),商店日利潤的期望值最大?并求出日利潤期望值的最大值.
為多少時(shí),商店日利潤的期望值最大?并求出日利潤期望值的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校為了增強(qiáng)學(xué)生的記憶力和辨識(shí)力,組織了一場類似《最強(qiáng)大腦》的PK賽,![]() 兩隊(duì)各由4名選手組成,每局兩隊(duì)各派一名選手PK,比賽四局.除第三局勝者得2分外,其余各局勝者均得1分,每局的負(fù)者得0分.假設(shè)每局比賽A隊(duì)選手獲勝的概率均為
兩隊(duì)各由4名選手組成,每局兩隊(duì)各派一名選手PK,比賽四局.除第三局勝者得2分外,其余各局勝者均得1分,每局的負(fù)者得0分.假設(shè)每局比賽A隊(duì)選手獲勝的概率均為![]() ,且各局比賽結(jié)果相互獨(dú)立,比賽結(jié)束時(shí)A隊(duì)的得分高于B隊(duì)的得分的概率為( )
,且各局比賽結(jié)果相互獨(dú)立,比賽結(jié)束時(shí)A隊(duì)的得分高于B隊(duì)的得分的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() 滿足:對(duì)任意實(shí)數(shù)
滿足:對(duì)任意實(shí)數(shù)![]() ,方程
,方程![]() 的解的個(gè)數(shù)為偶數(shù)(可以是0個(gè),但不能是無數(shù)個(gè)),則稱
的解的個(gè)數(shù)為偶數(shù)(可以是0個(gè),但不能是無數(shù)個(gè)),則稱![]() 為“偶的函數(shù)”.證明:
為“偶的函數(shù)”.證明:
(1)任何多項(xiàng)式![]() 均不是偶的函數(shù);
均不是偶的函數(shù);
(2)存在連續(xù)函數(shù)![]() 是偶的函數(shù).
是偶的函數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)n為一個(gè)正整數(shù),三維空間內(nèi)的點(diǎn)集S滿足下述性質(zhì):
(1).空間內(nèi)不存在n個(gè)平面,使得點(diǎn)集S中的每個(gè)點(diǎn)至少在這n個(gè)平面中的一個(gè)平面上;
(2).對(duì)于每個(gè)點(diǎn)![]() ,均存在n個(gè)平面,使得
,均存在n個(gè)平面,使得![]() 中的每個(gè)點(diǎn)均至少在這n個(gè)平面中的一個(gè)平面上.
中的每個(gè)點(diǎn)均至少在這n個(gè)平面中的一個(gè)平面上.
求點(diǎn)集S中點(diǎn)的個(gè)數(shù)的最小值與最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】進(jìn)入![]() 月份,香港大學(xué)自主招生開始報(bào)名,“五校聯(lián)盟”統(tǒng)一對(duì)五校高三學(xué)生進(jìn)行綜合素質(zhì)測試,在所有參加測試的學(xué)生中隨機(jī)抽取了部分學(xué)生的成績,得到如圖所示的成績頻率分布直方圖:
月份,香港大學(xué)自主招生開始報(bào)名,“五校聯(lián)盟”統(tǒng)一對(duì)五校高三學(xué)生進(jìn)行綜合素質(zhì)測試,在所有參加測試的學(xué)生中隨機(jī)抽取了部分學(xué)生的成績,得到如圖所示的成績頻率分布直方圖:
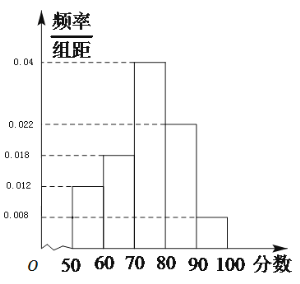
(1)估計(jì)五校學(xué)生綜合素質(zhì)成績的平均值;
(2)某校決定從本校綜合素質(zhì)成績排名前![]() 名同學(xué)中,推薦
名同學(xué)中,推薦![]() 人參加自主招生考試,若已知
人參加自主招生考試,若已知![]() 名同學(xué)中有
名同學(xué)中有![]() 名理科生,2名文科生,試求這3人中含文科生的概率.
名理科生,2名文科生,試求這3人中含文科生的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com