【題目】已知函數
在
與
時都取得極值.（1）求
的值；（2）若對
， 
恒成立，求
的取值范圍
【答案】(1) 
(2) 
【解析】試題分析：（1）求出導函數，通過
和
為
的兩根，得到方程組求解即可；（2）化簡函數
，求出導函數，通過當
時，當
時，當
時， 
，當
時， 
，判斷函數的單調性，求出函數的極值，然后求解
的取值范圍.
試題解析：（1）∵
，由已知條件可知： 
和1為
的兩根，
由韋達定理得：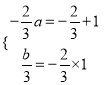 
，∴
， 
（2）由（1）得： 
，由題知：當
(－2， 
)時， 
∴函數
在區間(－2， 
)上是增函數；
當
(
，1)時， 
，∴函數
在(
，1)上是減函數；
當
(1，2)時， 
，∴函數
在(1，2)上是增函數，
∴當
時， 
；當
時， 
∵
，∴
[－2，2]時， 
，
由
在
[－2，2]時， 
恒成立得： 
由此解得： 
∴
的取值范圍為：(
， 
]∪[2， 
)
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】數列
的前
項和為
，
．
（
）證明數列
是等比數列，求出數列的通項公式．
（
）設
，求數列
的前項和
．
（
）數列中是否存在三項，它們可以構成等比數列？若存在，求出一組符合條件的項；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（題文）（題文）“你低碳了嗎？”這是某市為倡導建設節約型社會而發布的公益廣告里的一句話，活動組織者為了了解這則廣告的宣傳效果，隨機抽取了120名年齡在
，
，…，
的市民進行問卷調查，由此得到的樣本的頻率分布直方圖如圖所示.
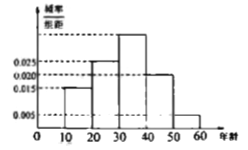
（1）根據直方圖填寫頻率分布統計表；
（2）根據直方圖，試估計受訪市民年齡的中位數（保留整數）；
（3）如果按分層抽樣的方法，在受訪市民樣本年齡在
中共抽取5名市民，再從這5人中隨機選2人作為本次活動的獲獎者，求年齡在
和的受訪市民恰好各有一人獲獎的概率.
分組 | 頻數 | 頻率 |
| 18 | 0.15 |
| 30 | |
| ||
| 0.2 | |
| 6 | 0.05 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的上下兩個焦點分別為
，過點
與
軸垂直的直線交橢圓
于
兩點， 
的面積為
，橢圓
的離心率為
．
（1）求橢圓
的標準方程；
（2）已知
為坐標原點，直線
與
軸交于點
，與橢圓
交于
兩個不同的點，若
，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
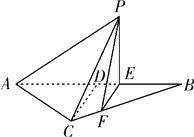
【題目】如圖所示，等腰
的底邊
，高
，點
是線段
上異于點
的動點，點
在
邊上，且
，現沿
將△
折起到△
的位置，使
，記
， 
表示四棱錐
的體積．
(1)求
的表達式；(2)當
為何值時， 
取得最大,并求最大值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
.
（1）當
時，求函數
的最大值；
（2）令
，其圖象上存在一點
，使此處切線的斜率
，求實數
的取值范圍；
（3）當
， 
時，方程
有唯一實數解，求正數
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正方形
的中心為點
, 
邊所在的直線方程為
.
（1）求
邊所在的直線方程和正方形
外接圓的方程；
（2）若動圓
過點
,且與正方形
外接圓外切,求動圓圓心
的軌跡方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
