
【題目】“累積凈化量(![]() )”是空氣凈化器質量的一個重要衡量指標,它是指空氣凈化器從開始使用到凈化效率為
)”是空氣凈化器質量的一個重要衡量指標,它是指空氣凈化器從開始使用到凈化效率為![]() 時對顆粒物的累積凈化量,以克表示.根據
時對顆粒物的累積凈化量,以克表示.根據![]() 《空氣凈化器》國家標準,對空氣凈化器的累計凈化量(
《空氣凈化器》國家標準,對空氣凈化器的累計凈化量(![]() )有如下等級劃分:
)有如下等級劃分:
累積凈化量(克) |
|
|
| 12以上 |
等級 |
|
|
|
|
為了了解一批空氣凈化器(共2000臺)的質量,隨機抽取![]() 臺機器作為樣本進行估計,已知這
臺機器作為樣本進行估計,已知這![]() 臺機器的累積凈化量都分布在區間
臺機器的累積凈化量都分布在區間![]() 中.按照
中.按照![]() 均勻分組,其中累積凈化量在
均勻分組,其中累積凈化量在![]() 的所有數據有:
的所有數據有: ![]() 和
和![]() ,并繪制了如下頻率分布直方圖:
,并繪制了如下頻率分布直方圖:

(1)求![]() 的值及頻率分布直方圖中的
的值及頻率分布直方圖中的![]() 值;
值;
(2)以樣本估計總體,試估計這批空氣凈化器(共2000臺)中等級為![]() 的空氣凈化器有多少臺?
的空氣凈化器有多少臺?
(3)從累積凈化量在![]() 的樣本中隨機抽取2臺,求恰好有1臺等級為
的樣本中隨機抽取2臺,求恰好有1臺等級為![]() 的概率.
的概率.
【答案】(1)![]() (2)這批空氣凈化器等級為
(2)這批空氣凈化器等級為![]() 的空氣凈化器共有560臺. (3)
的空氣凈化器共有560臺. (3)![]()
【解析】【試題分析】(1)依據頻率分布直方圖分析求解;(2)依據題設借助頻率分布直方圖求解;(3)運用列舉法及古典概型的計算公式分析求解:
(Ⅰ)因為![]() 之間的數據一共有6個,
之間的數據一共有6個,
再由頻率分布直方圖可知:落在![]() 之間的頻率為
之間的頻率為![]() .
.
因此, ![]() .
.
![]() ∴
∴![]() .
.
(Ⅱ)由頻率分布直方圖可知:落在![]() 之間共:
之間共: ![]() 臺,
臺,
又因為在![]() 之間共4臺,
之間共4臺,
∴落在![]() 之間共28臺,
之間共28臺,
故,這批空氣凈化器等級為![]() 的空氣凈化器共有560臺.
的空氣凈化器共有560臺.
(Ⅲ)設“恰好有1臺等級為![]() ”為事件
”為事件![]()
依題意,落在![]() 之間共有6臺.記為:
之間共有6臺.記為: ![]() ,屬于國標
,屬于國標![]() 級有4臺,我們記為:
級有4臺,我們記為: ![]() ,
,
則從![]() 中隨機抽取2個,所有可能的結果有15種,它們是:
中隨機抽取2個,所有可能的結果有15種,它們是: ![]()
![]()
![]()
![]()
![]() ,
,
而事件![]() 的結果有8種,它們是:
的結果有8種,它們是: ![]()
![]()
![]() .
.
因此事件![]() 的概率為
的概率為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.
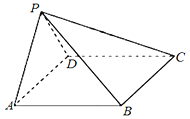
(1).證明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱錐PABCD的體積為![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 在橢圓
在橢圓![]() 上,且橢圓的離心率為
上,且橢圓的離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 為橢圓
為橢圓![]() 的右頂點,點
的右頂點,點![]() 是橢圓
是橢圓![]() 上不同的兩點(均異于
上不同的兩點(均異于![]() )且滿足直線
)且滿足直線![]() 與
與![]() 斜率之積為
斜率之積為![]() .試判斷直線
.試判斷直線![]() 是否過定點,若是,求出定點坐標,若不是,說明理由.
是否過定點,若是,求出定點坐標,若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
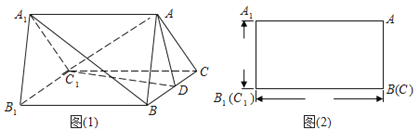
【題目】如圖(1)是一個水平放置的正三棱柱![]() ,
, ![]() 是棱
是棱![]() 的中點.正三棱柱的正(主)視圖如圖(2).
的中點.正三棱柱的正(主)視圖如圖(2).
(Ⅰ)求正三棱柱![]() 的體積;
的體積;
(Ⅱ)證明: ![]() ;
;
(Ⅲ)圖(1)中垂直于平面![]() 的平面有哪幾個?(直接寫出符合要求的平面即可,不必說明或證明)
的平面有哪幾個?(直接寫出符合要求的平面即可,不必說明或證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人參加微信群搶紅包游戲,規則如下:每輪游戲發![]() 個紅包,每個紅包金額為
個紅包,每個紅包金額為![]() 元,
元,![]() .已知在每輪游戲中所產生的
.已知在每輪游戲中所產生的![]() 個紅包金額的頻率分布直方圖如圖所示.
個紅包金額的頻率分布直方圖如圖所示.
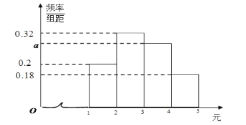
(1)求![]() 的值,并根據頻率分布直方圖,估計紅包金額的眾數;
的值,并根據頻率分布直方圖,估計紅包金額的眾數;
(2)以頻率分布直方圖中的頻率作為概率,若甲、乙、丙三人從中各搶到一個紅包,其中金額在![]() 的紅包個數為
的紅包個數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】地為綠化環境,移栽了銀杏樹![]() 棵,梧桐樹
棵,梧桐樹![]() 棵.它們移栽后的成活率分別
棵.它們移栽后的成活率分別
為![]() 、
、![]() ,每棵樹是否存活互不影響,在移栽的
,每棵樹是否存活互不影響,在移栽的![]() 棵樹中:
棵樹中:
(1)求銀杏樹都成活且梧桐樹成活![]() 棵的概率;
棵的概率;
(2)求成活的棵樹![]() 的分布列與期望.
的分布列與期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的準線與
的準線與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 做圓
做圓![]() 的兩條切線,切點為
的兩條切線,切點為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若直線![]() 是講過定點
是講過定點![]() 的一條直線,且與拋物線
的一條直線,且與拋物線![]() 交于
交于![]() 兩點,過定點
兩點,過定點![]() 作
作![]() 的垂線與拋物線交于
的垂線與拋物線交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左焦點
的左焦點![]() 與拋物線
與拋物線![]() 的焦點重合,橢圓
的焦點重合,橢圓![]() 的離心率為
的離心率為![]() ,過點
,過點![]() 作斜率不為0的直線
作斜率不為0的直線![]() ,交橢圓
,交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() ,且
,且![]() 為定值.
為定值.
(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() , 若橢圓上一點
, 若橢圓上一點![]() 滿足
滿足![]() ,且橢圓
,且橢圓![]() 過點
過點![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 是點
是點![]() 在
在![]() 軸上的垂足,延長
軸上的垂足,延長![]() 交橢圓
交橢圓![]() 于
于![]() ,求證:
,求證: ![]() 三點共線.
三點共線.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com