
【題目】已知函數(shù)![]() ,函數(shù)
,函數(shù)![]() 的導函數(shù)
的導函數(shù)![]() ,且
,且![]() ,其中
,其中![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(Ⅰ)求![]() 的極值;
的極值;
(Ⅱ)若存在![]() ,使得不等式
,使得不等式![]() 成立,試求實數(shù)
成立,試求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)當![]() 時,對于
時,對于![]() ,求證:
,求證:![]() .
.
【答案】(Ⅰ)見解析(Ⅱ)![]() (Ⅲ)見解析
(Ⅲ)見解析
【解析】
(Ⅰ)求導,對![]() 進行分類討論,研究單調(diào)性,求極值.
進行分類討論,研究單調(diào)性,求極值.
(Ⅱ)先求得![]() ,分離變量,即
,分離變量,即![]() ,構(gòu)造新函數(shù),求其最大值,即可求出
,構(gòu)造新函數(shù),求其最大值,即可求出![]() 的取值范圍.
的取值范圍.
(Ⅲ)令![]() ,即
,即![]() ,求導研究單調(diào)性,求最小值大于0即可證得原不等式成立.
,求導研究單調(diào)性,求最小值大于0即可證得原不等式成立.
(Ⅰ)函數(shù)![]() 的定義域為
的定義域為![]() ,
,![]() .
.
當![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),![]() 沒有極值;
沒有極值;
當![]() 時,令
時,令![]()
∴![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減
單調(diào)遞減
∴![]() 有極大值
有極大值![]() ,無極小值.
,無極小值.
(Ⅱ)![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]()
∴![]()
∵![]() ,使得不等式
,使得不等式![]() 成立
成立
即![]()
令![]() ,
,![]()
當![]() 時,
時,![]() ,
,![]()
∴![]() ,即
,即![]() .
.
∴![]() 在
在![]() 單調(diào)遞減,∴
單調(diào)遞減,∴![]()
∴![]() .
.
(Ⅲ)當![]() 時,
時,![]() ,令
,令![]() ,
,
即![]()
∴![]() ,則
,則![]() 在
在![]() 上為增函數(shù)
上為增函數(shù)
∵![]() ,
,![]()
∴![]() .∵
.∵![]() 在
在![]() 上為增函數(shù)
上為增函數(shù)
∴![]() 時,
時,![]() ,
,![]() 時,
時,![]() .
.
![]() 在
在![]() 單調(diào)遞減,在
單調(diào)遞減,在![]() 單調(diào)遞增
單調(diào)遞增
∴![]()
∵![]() ∴
∴![]()
∵![]() ∴
∴![]() 單調(diào)遞減,
單調(diào)遞減,
∴![]()
∴![]() 即
即![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】某電視臺為了了解某社區(qū)居民對某娛樂節(jié)目的收視情況,隨機抽取了![]() 名觀眾進行調(diào)查,下面是根據(jù)調(diào)查結(jié)果繪制的觀眾日均收看該娛樂節(jié)目時間的頻率分布直方圖:
名觀眾進行調(diào)查,下面是根據(jù)調(diào)查結(jié)果繪制的觀眾日均收看該娛樂節(jié)目時間的頻率分布直方圖:
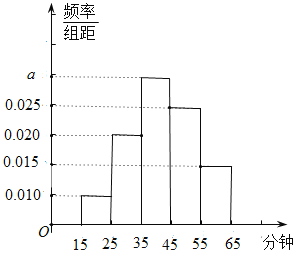
(1)求實數(shù)![]() 的值;
的值;
(2)根據(jù)統(tǒng)計結(jié)果,試估計觀眾觀看該娛樂節(jié)目時間的中位數(shù)(結(jié)果保留一位小數(shù));
(3)從觀看時間在![]() ,
,![]() 的人中用分層抽樣的方法抽取6人,再從這6人中隨機抽取2人,求這2人的觀看時間都在
的人中用分層抽樣的方法抽取6人,再從這6人中隨機抽取2人,求這2人的觀看時間都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某學生對其親屬30人的飲食習慣進行了一次調(diào)查,并用下圖所示的莖葉圖表示30人的飲食指數(shù).(說明:圖中飲食指數(shù)低于70的人,飲食以蔬菜為主;飲食指數(shù)高于70的人,飲食以肉類為主)
(1)根據(jù)以上數(shù)據(jù)完成下面的2×2列聯(lián)表:
主食 蔬菜 | 主食 肉類 | 總計 | |
50歲以下 | |||
50歲以上 | |||
總計 |
(2)能否在犯錯誤的概率不超過0.010的前提下認為“其親屬的飲食習慣與年齡有關(guān)”?并寫出簡要分析.
附參考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知集合A={x|1-a≤x≤1+a}(a>0),B={x|x2-5x+4≤0}.
(1)若“x∈A”是“x∈B”的必要不充分條件,求實數(shù)a的取值范圍;
(2)對任意x∈B,不等式x2-mx+4≥0都成立,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
,![]() ,以
,以![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() ,連接
,連接![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)若二面角![]() 為
為![]() .
.
求證:平面![]() 平面
平面![]() ;
;
求直線![]() 與平面
與平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 滿足對任意的
滿足對任意的![]() 都有
都有![]() ,且
,且![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)設(shè)數(shù)列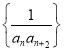 的前
的前![]() 項和為
項和為![]() ,不等式
,不等式![]() 對任意的正整數(shù)
對任意的正整數(shù)![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com