
【題目】已知數列{an}滿足a1=1,an+1=3an+4,n∈N*.
(1)證明:數列{an+2}是等比數列,并求數列{an}的通項公式;
(2)設bn=(a2n+2)log3(an+2),求數列{bn}的前n項和Tn.
科目:高中數學 來源: 題型:
【題目】某企業開發一種新產品,現準備投入適當的廣告費對產品進行促銷,在一年內,預計年銷量![]() (萬件)與廣告費
(萬件)與廣告費![]() (萬元)之間的函數關系為
(萬元)之間的函數關系為![]() ,已知生產此產品的年固定投入為
,已知生產此產品的年固定投入為![]() 萬元,每生產
萬元,每生產![]() 萬件此產品仍需要投入
萬件此產品仍需要投入![]() 萬元,若年銷售額為“年生產成本的
萬元,若年銷售額為“年生產成本的![]() ”與“年廣告費的
”與“年廣告費的![]() ”之和,而當年產銷量相等:
”之和,而當年產銷量相等:
(1)試將年利潤![]() (萬元)表示為年廣告費
(萬元)表示為年廣告費![]() (萬元)的函數;
(萬元)的函數;
(2)求當年廣告費投入多少萬元時,企業利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位有員工1000名,平均每人每年創造利潤10萬元.為增加企業競爭力,決定優化產業結構,調整出![]() 名員工從事第三產業,調整后平均每人每年創造利潤為
名員工從事第三產業,調整后平均每人每年創造利潤為![]() 萬元
萬元![]() ,剩下的員工平均每人每年創造的利潤可以提高
,剩下的員工平均每人每年創造的利潤可以提高![]() .
.
(1)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤,則最多調整出多少名員工從事第三產業?
(2)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤條件下,若要求調整出的員工創造出的年總利潤始終不高于剩余員工創造的年總利潤,則![]() 的取值范圍是多少?
的取值范圍是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的公差d≠0,且a1,a3,a13成等比數列,若a1=1,Sn為數列{an}的前n項和,則![]() 的最小值為( )
的最小值為( )
A.4B.3C.![]() D.2
D.2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應黨中央“扶貧攻堅”的號召,某單位指導一貧困村通過種植紫甘薯來提高經濟收入.紫甘薯對環境溫度要求較高,根據以往的經驗,隨著溫度的升高,其死亡株數成增長的趨勢.下表給出了2017年種植的一批試驗紫甘薯在溫度升高時6組死亡的株數:

經計算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 分別為試驗數據中的溫度和死亡株數,
分別為試驗數據中的溫度和死亡株數, ![]() .
.
(1)若用線性回歸模型,求![]() 關于
關于![]() 的回歸方程
的回歸方程![]() (結果精確到
(結果精確到![]() );
);
(2)若用非線性回歸模型求得![]() 關于
關于![]() 的回歸方程為
的回歸方程為![]() ,且相關指數為
,且相關指數為![]() .
.
(i)試與(1)中的回歸模型相比,用![]() 說明哪種模型的擬合效果更好;
說明哪種模型的擬合效果更好;
(ii)用擬合效果好的模型預測溫度為![]() 時該批紫甘薯死亡株數(結果取整數).
時該批紫甘薯死亡株數(結果取整數).
附:對于一組數據![]() ,
, ![]() ,……,
,……, ![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:  ;相關指數為:
;相關指數為:  .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD為菱形,且∠ABC=60°,
中,底面ABCD為菱形,且∠ABC=60°,![]() 平面ABCD,
平面ABCD,![]() ,點E,F為PC,PA的中點.
,點E,F為PC,PA的中點.
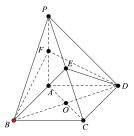
(1)求證:平面BDE⊥平面ABCD;
(2)二面角E—BD—F的大小;
(3)設點M在PB(端點除外)上,試判斷CM與平面BDF是否平行,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】鄭州一中社團為調查學生學習圍棋的情況,隨機抽取了100名學生進行調查.根據調查結果繪制的學生日均學習圍棋時間的頻率分布直方圖:將日均學習圍棋時間不低于40分鐘的學生稱為“圍棋迷”.
(1)根據已知條件完成下面的2×2列聯表,并據此資料你是否認為“圍棋迷”與性別有關?

非圍棋迷 | 圍棋迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
(2)將上述調查所得到的頻率視為概率.現在從該地區大量學生中,采用隨機抽樣方法每次抽取1名學生,抽取3次,記被抽取的3名學生中的“圍棋迷”人數為![]() .若每次抽取的結果是相互獨立的,求
.若每次抽取的結果是相互獨立的,求![]() 的分布列,期望
的分布列,期望
附:![]() ,
,
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com