
【題目】在![]() 中,點
中,點![]() ,角
,角![]() 的內(nèi)角平分線所在直線的方程為
的內(nèi)角平分線所在直線的方程為![]() ,
,![]() 邊上的高所在直線的方程為
邊上的高所在直線的方程為![]() .
.
(1)求點![]() 的坐標(biāo);
的坐標(biāo);
(2)求![]() 的內(nèi)切圓圓心.
的內(nèi)切圓圓心.
【答案】(1)![]() .(2)
.(2)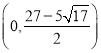
【解析】
(1)根據(jù)題意可得![]() 的斜率為
的斜率為![]() ,從而可得直線
,從而可得直線![]() 的方程;將
的方程;將![]() 與
與![]() 聯(lián)立求出點
聯(lián)立求出點![]() 的坐標(biāo),再根據(jù)點
的坐標(biāo),再根據(jù)點![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點
的對稱點![]() 在直線
在直線![]() 上,求出直線
上,求出直線![]() 的方程,將
的方程,將![]() 的方程與
的方程與![]() 的方程聯(lián)立即可求出點
的方程聯(lián)立即可求出點![]() 的坐標(biāo).
的坐標(biāo).
(2)內(nèi)切圓圓心為三角形內(nèi)角平分線的交點,設(shè)內(nèi)切圓圓心為![]() ,利用點到直線的距離公式可得
,利用點到直線的距離公式可得![]() ,從而可求出
,從而可求出![]() ,再根據(jù)直線
,再根據(jù)直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,即可求得
,即可求得![]() .
.
(1)由題意知![]() 的斜率為
的斜率為![]() ,又點
,又點![]() ,
,
∴直線![]() 的方程為
的方程為![]() ,即
,即![]() .
.
解方程組![]() ,得
,得![]()
∴點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
又![]() 的內(nèi)角平分線所在直線的方程為
的內(nèi)角平分線所在直線的方程為![]() ,
,
∴點![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點
的對稱點![]() 在直線
在直線![]() 上,
上,
∴直線![]() 的方程為
的方程為![]() ,即
,即![]()
解方程組![]() ,得
,得![]()
∴點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
(2)內(nèi)切圓圓心為三角形內(nèi)角平分線的交點
∴設(shè)內(nèi)切圓圓心為![]()
∴![]()
∴![]()
解得:![]()
又直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,
,![]() ,
,![]()
結(jié)合圖形可知:![]() 舍去
舍去
∴![]() 的內(nèi)切圓圓心為
的內(nèi)切圓圓心為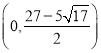 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知某地一天從![]() 時的溫度變化曲線近似滿足函數(shù)
時的溫度變化曲線近似滿足函數(shù)![]() .
.
(1)求該地區(qū)這一段時間內(nèi)溫度的最大溫差.
(2)若有一種細(xì)菌在![]() 到
到![]() 之間可以生存,則在這段時間內(nèi),該細(xì)菌最多能存活多長時間?
之間可以生存,則在這段時間內(nèi),該細(xì)菌最多能存活多長時間?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是矩形,側(cè)棱
是矩形,側(cè)棱![]() 底面
底面![]() ,且
,且![]() ,
,![]() 為棱
為棱![]() 的中點,作
的中點,作![]() 交
交![]() 于點
于點![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)若面![]() 與面
與面![]() 所成二面角的大小為
所成二面角的大小為![]() ,求
,求![]() 與面
與面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】通過市場調(diào)查,得到某種產(chǎn)品的資金投入![]() (單位:萬元)與獲得的利潤
(單位:萬元)與獲得的利潤![]() (單位:千元)的數(shù)據(jù),如表所示
(單位:千元)的數(shù)據(jù),如表所示
資金投入 | 2 | 3 | 4 | 5 |
利潤 | 2 | 3 | 5 | 6 |
(1)根據(jù)上表提供的數(shù)據(jù),用最小二乘法求線性回歸直線方程![]() ;
;
(2)該產(chǎn)品的資金投入每增加![]() 萬元,獲得利潤預(yù)計可增加多少千元?若投入資金
萬元,獲得利潤預(yù)計可增加多少千元?若投入資金![]() 萬元,則獲得利潤的估計值為多少千元?
萬元,則獲得利潤的估計值為多少千元?
參考公式:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙、丙、丁四位同學(xué)中僅有一人申請了北京大學(xué)的自主招生考試,當(dāng)他們被問到誰申請了北京大學(xué)的自主招生考試時,甲說:“丙或丁申請了”;乙說:“丙申請了”;丙說:“甲和丁都沒有申請”;丁說:“乙申請了”,如果這四位同學(xué)中只有兩人說的是對的,那么申請了北京大學(xué)的自主招生考試的同學(xué)是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知直線
中,已知直線![]() :
: (
(![]() 為參數(shù)).以坐標(biāo)原點
為參數(shù)).以坐標(biāo)原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點![]() 的直角坐標(biāo)為
的直角坐標(biāo)為![]() ,直線
,直線![]() 與曲線
與曲線![]() 的交點為
的交點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在第二屆烏鎮(zhèn)互聯(lián)網(wǎng)大會中, 為了提高安保的級別同時又為了方便接待,現(xiàn)將其中的五個參會國的人員安排酒店住宿,這五個參會國要在![]() 、
、![]() 、
、![]() 三家酒店選擇一家,且每家酒店至少有一個參會國入住,則這樣的安排方法共有
三家酒店選擇一家,且每家酒店至少有一個參會國入住,則這樣的安排方法共有
A.![]() 種B.
種B.![]() 種
種
C.![]() 種D.
種D.![]() 種
種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
![]() 若
若![]() 是函數(shù)
是函數(shù)![]() 的極值點,求曲線
的極值點,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
![]() 若函數(shù)
若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上為單調(diào)遞減函數(shù),求實數(shù)a的取值范圍;
上為單調(diào)遞減函數(shù),求實數(shù)a的取值范圍;
![]() 設(shè)m,n為正實數(shù),且
設(shè)m,n為正實數(shù),且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分16分)設(shè)數(shù)列![]() 的前n項和為
的前n項和為![]() ,數(shù)列
,數(shù)列![]() 滿足:
滿足:![]() ,且數(shù)列
,且數(shù)列![]() 的前
的前
n項和為![]() .
.
(1) 求![]() 的值;
的值;
(2) 求證:數(shù)列![]() 是等比數(shù)列;
是等比數(shù)列;
(3) 抽去數(shù)列![]() 中的第1項,第4項,第7項,……,第3n-2項,……余下的項順序不變,組成一個新數(shù)列
中的第1項,第4項,第7項,……,第3n-2項,……余下的項順序不變,組成一個新數(shù)列![]() ,若
,若![]() 的前n項和為
的前n項和為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com