
【題目】已知公差不為零的等差數列{an)滿足a1=5,且a3,a6,a11成等比數列.
(1)求數列{an}的通項公式;
(2)設bn=an·3n-1,求數列{bn}的前n項和Sn.
【答案】(1)an=2n+3; (2)Sn=(n+1)×3n-1.
【解析】
(1)根據等差數列![]() 中,
中,![]() ,且
,且![]() 成等比數列列出關于公差
成等比數列列出關于公差![]() 的方程,解方程可得
的方程,解方程可得![]() 的值,從而可得數列
的值,從而可得數列![]() 的通項公式;(2)由(1)可得
的通項公式;(2)由(1)可得![]() ,利用錯位相減法,結合等比數列的求和公式,即可得結果.
,利用錯位相減法,結合等比數列的求和公式,即可得結果.
(1)設等差數列{an}的公差為d,因為a3,a6,a11成等比數列,
所以![]() ,即(a1+5d)2=(a1+2d)(a1+10d),
,即(a1+5d)2=(a1+2d)(a1+10d),
化簡得5d-2a1=0.
又a1=5,所以d=2,從而an=2n+3.
(2)由(1)可得![]() ,
,
所以Sn=5×30+7×31+9×32+…+![]()
所以3Sn=5×31+7×32+9×33+…+(2n+3)×3n,
以上兩個等式相減得![]() ,
,
化簡得Sn=(n+1)×3n-1


科目:高中數學 來源: 題型:
【題目】如圖所示,![]() 為平行四邊形ABCD所在平面外一點,M,N分別為AB,PC的中點,平面PAD
為平行四邊形ABCD所在平面外一點,M,N分別為AB,PC的中點,平面PAD![]() 平面PBC=
平面PBC=![]() .
.
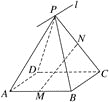
(1)求證:BC∥![]() ;
;
(2)MN與平面PAD是否平行?試證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在直角坐標系xOy中,直線 ![]() 的參數方程為
的參數方程為 ![]() (t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線C的直角坐標方程;
的普通方程和曲線C的直角坐標方程;
(2)設點P是曲線C上的一個動點,求它到直線![]() 的距離d的取值范圍.
的距離d的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 在R上是增函數,求實數a的取值范圍;
在R上是增函數,求實數a的取值范圍;
(2)求所有的實數a,使得對任意![]() 時,函數
時,函數![]() 的圖象恒在函數
的圖象恒在函數![]() 圖象的下方;
圖象的下方;
(3)若存在![]() ,使得關于x的方程
,使得關于x的方程![]() 有三個不相等的實數根,求實數t的取值范圍.
有三個不相等的實數根,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大衍數列,來源于《乾坤譜》中對易傳“大衍之數五十“的推論.主要用于解釋中國傳統文化中的太極衍生原理數列中的每一項,都代表太極衍生過程中,曾經經歷過的兩儀數量總和是中華傳統文化中隱藏著的世界數學史上第一道數列題其規律是:偶數項是序號平方再除以2,奇數項是序號平方減1再除以2,其前10項依次是0,2,4,8,12,18,24,32,40,50,…,如圖所示的程序框圖是為了得到大衍數列的前100項而設計的,那么在兩個判斷框中,可以先后填入( )

A. ![]() 是偶數?,
是偶數?,![]() ? B.
? B. ![]() 是奇數?,
是奇數?,![]() ?
?
C. ![]() 是偶數?,
是偶數?, ![]() ? D.
? D. ![]() 是奇數?,
是奇數?,![]() ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知質點P繞點M逆時針做勻速圓周運動(如圖1),質點P相對于水平直線l的位置用y(米)表示,質點在l上方時,y為正,反之,y為負,![]() 是質點與直線l的距離,位置y與時間t(秒)之間的關系為
是質點與直線l的距離,位置y與時間t(秒)之間的關系為![]() (其中
(其中![]() ,
,![]() ,
,![]() )其圖象如圖2所示.
)其圖象如圖2所示.

(1)寫出質點P運動的圓形軌道半徑及從初始位置到最高點所需要的時間;
(2)求![]() 的解析式,并指出質點P第二次出現在直線l上的時刻.
的解析式,并指出質點P第二次出現在直線l上的時刻.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從岳陽到郴州的快速列車包括起始站和終點站共有六站,將這六站分別記為![]() .有一天,張兵和其他18 名旅客乘同一車廂離開岳陽,這些旅客中有些是湖北人,其他的是湖南人,認識所有同車廂旅客的張兵觀測到:除了終點站,在每一站,當火車到達時,這節車廂上的湖南人的數目與下車旅客的數目相同,且這次行程中沒有新的旅客進入這節車廂.張兵又進一步觀測到:當火車離開
.有一天,張兵和其他18 名旅客乘同一車廂離開岳陽,這些旅客中有些是湖北人,其他的是湖南人,認識所有同車廂旅客的張兵觀測到:除了終點站,在每一站,當火車到達時,這節車廂上的湖南人的數目與下車旅客的數目相同,且這次行程中沒有新的旅客進入這節車廂.張兵又進一步觀測到:當火車離開![]() 站時,車廂內有 12名旅客;當火車離開
站時,車廂內有 12名旅客;當火車離開![]() 站時,還有 7 名旅客在這一車廂內;當他準備在
站時,還有 7 名旅客在這一車廂內;當他準備在![]() 站下車時,還有5名旅客在這一車廂內.試問開始時火車的這一節車廂有多少湖北人,有多少湖南人?且在旅途中這些數目如何變化?
站下車時,還有5名旅客在這一車廂內.試問開始時火車的這一節車廂有多少湖北人,有多少湖南人?且在旅途中這些數目如何變化?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com