
【題目】已知函數(shù)![]() .
.
(1)若函數(shù)![]() 在R上是增函數(shù),求實數(shù)a的取值范圍;
在R上是增函數(shù),求實數(shù)a的取值范圍;
(2)求所有的實數(shù)a,使得對任意![]() 時,函數(shù)
時,函數(shù)![]() 的圖象恒在函數(shù)
的圖象恒在函數(shù)![]() 圖象的下方;
圖象的下方;
(3)若存在![]() ,使得關(guān)于x的方程
,使得關(guān)于x的方程![]() 有三個不相等的實數(shù)根,求實數(shù)t的取值范圍.
有三個不相等的實數(shù)根,求實數(shù)t的取值范圍.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)將函數(shù)寫成分段函數(shù)的性質(zhì),根據(jù)分段函數(shù)在![]() 上是單調(diào)增函數(shù),即可求得參數(shù)的范圍;
上是單調(diào)增函數(shù),即可求得參數(shù)的范圍;
(2)根據(jù)題意,分離參數(shù),將問題轉(zhuǎn)化求解函數(shù)在區(qū)間上最值的問題,即可求得;
(3)將方程根的個數(shù)的問題,轉(zhuǎn)化為函數(shù)圖像交點個數(shù)的問題,求出函數(shù)的值域,結(jié)合函數(shù)的單調(diào)性即可求得.
(1)∵函數(shù) .
.
由于![]() 在R上是連續(xù)的增函數(shù),
在R上是連續(xù)的增函數(shù),
所以只要當(dāng)![]() 時為增函數(shù)且當(dāng)
時為增函數(shù)且當(dāng)![]() 時也為增函數(shù);
時也為增函數(shù);
即 ,解得
,解得![]() ,則a的范圍為
,則a的范圍為![]() .
.
(2)由題意得對任意的實數(shù)![]() ,
,![]() 恒成立,
恒成立,
即![]() ,當(dāng)
,當(dāng)![]() 恒成立,
恒成立,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() 且
且![]() 在
在![]() 上恒成立,
上恒成立,
即在![]() 時,只要
時,只要![]() 的最大值且
的最大值且![]() 的最小值即可,
的最小值即可,
而當(dāng)![]() 時,
時,![]() 為增函數(shù),
為增函數(shù),![]() ;
;
當(dāng)![]() 時,
時,![]() 為增函數(shù),
為增函數(shù),![]() ,
,
∴![]() .
.
所以滿足條件的所有![]() .
.
(3)由題意得,關(guān)于x的方程![]() 有三個不相等的實數(shù)根
有三個不相等的實數(shù)根
![]() 有三個不相等的實數(shù)根;
有三個不相等的實數(shù)根;
即![]() 與
與![]() 有三個不同的交點;
有三個不同的交點;
①當(dāng)![]() 時,由(1)知,
時,由(1)知,![]() 在R上是增函數(shù),
在R上是增函數(shù),
則關(guān)于x的方程![]() 不可能有三個不等的實數(shù)根;
不可能有三個不等的實數(shù)根;
②當(dāng)![]() 時,由
時,由 .
.
當(dāng)![]() 時,∵
時,∵![]() ,
,
∴![]() 對稱軸
對稱軸![]() ,
,
則![]() 在
在![]() 為增函數(shù);
為增函數(shù);
此時![]() 的值域為
的值域為![]() ,
,
當(dāng)![]() 時,
時,![]() 對稱軸
對稱軸![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴對稱軸![]() ,
,
則![]() 在
在![]() 為增函數(shù),此時
為增函數(shù),此時![]() 的值域為
的值域為 ,
,
![]() 在
在![]() 為減函數(shù),此時
為減函數(shù),此時![]() 的值域為
的值域為 ;
;
綜上所述,若存在![]() ,使
,使![]() 與
與![]() 有三個不同的交點,
有三個不同的交點,
則![]() ,
,
即存在![]() ,使得
,使得![]() 即可,
即可,
令 ,
,
只要使![]() 即可,而
即可,而![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
![]() .
.
故可得![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,函數(shù)
,函數(shù)![]() ,函數(shù)
,函數(shù)![]() .
.
(1)當(dāng)函數(shù)![]() 圖象與
圖象與![]() 軸相切時,求實數(shù)
軸相切時,求實數(shù)![]() 的值;
的值;
(2)若函數(shù)![]() 對
對![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)當(dāng)![]() 時,討論函數(shù)
時,討論函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的零點個數(shù).
上的零點個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩位同學(xué)參加詩詞大賽,各答3道題,每人答對每道題的概率均為![]() ,且各人是否答對每道題互不影響.
,且各人是否答對每道題互不影響.
(Ⅰ)用![]() 表示甲同學(xué)答對題目的個數(shù),求隨機變量
表示甲同學(xué)答對題目的個數(shù),求隨機變量![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(Ⅱ)設(shè)![]() 為事件“甲比乙答對題目數(shù)恰好多2”,求事件
為事件“甲比乙答對題目數(shù)恰好多2”,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校實行選科走班制度,張毅同學(xué)的選擇是物理、生物、政治這三科,且物理在A層班級,生物在B層班級,該校周一上午課程安排如表所示,張毅選擇三個科目的課各上一節(jié),另外一節(jié)上自習(xí),則他不同的選課方法有( )
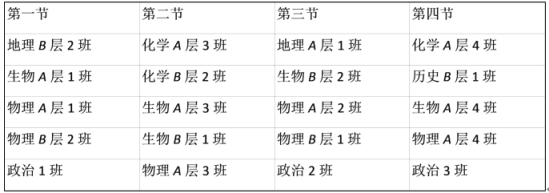
A.8種B.10種C.12種D.14種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
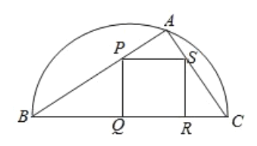
【題目】如圖,某園林單位準(zhǔn)備綠化一塊直徑為BC的半圓形空地,![]() 外的地方種草,
外的地方種草,![]() 的內(nèi)接正方形PQRS為一水池,其余的地方種花.若
的內(nèi)接正方形PQRS為一水池,其余的地方種花.若![]() ,
,![]() ,設(shè)
,設(shè)![]() 的面積為
的面積為![]() ,正方形PQRS的面積為
,正方形PQRS的面積為![]() .
.
(1)用a,![]() 表示
表示![]() 和
和![]() ;
;
(2)當(dāng)a為定值,![]() 變化時,求
變化時,求![]() 的最小值,及此時的
的最小值,及此時的![]() 值.
值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 在
在![]() 處取得極值.
處取得極值.
(Ⅰ)求函數(shù)![]() 的解析式;
的解析式;
(Ⅱ)求證:對于區(qū)間![]() 上任意兩個自變量的值
上任意兩個自變量的值![]() ,都有
,都有![]() ;
;
(Ⅲ)若過點![]() 可作曲線
可作曲線![]() 的三條切線,求實數(shù)
的三條切線,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知公差不為零的等差數(shù)列{an)滿足a1=5,且a3,a6,a11成等比數(shù)列.
(1)求數(shù)列{an}的通項公式;
(2)設(shè)bn=an·3n-1,求數(shù)列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
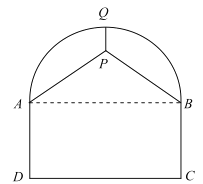
【題目】如圖,某隧道的剖面圖是由半圓及矩形![]() 組成,交通部門擬在隧道頂部安裝通風(fēng)設(shè)備(視作點
組成,交通部門擬在隧道頂部安裝通風(fēng)設(shè)備(視作點![]() ),為了固定該設(shè)備,計劃除從隧道最高點
),為了固定該設(shè)備,計劃除從隧道最高點![]() 處使用鋼管垂直向下吊裝以外,再在兩側(cè)自
處使用鋼管垂直向下吊裝以外,再在兩側(cè)自![]() 兩點分別使用鋼管支撐.已知道路寬
兩點分別使用鋼管支撐.已知道路寬![]() ,設(shè)備要求安裝在半圓內(nèi)部,所使用的鋼管總長度為
,設(shè)備要求安裝在半圓內(nèi)部,所使用的鋼管總長度為![]() .
.
(1)①設(shè)![]() ,將
,將![]() 表示為關(guān)于
表示為關(guān)于![]() 的函數(shù);
的函數(shù);
②設(shè)![]() ,將
,將![]() 表示為關(guān)于
表示為關(guān)于![]() 的函數(shù);
的函數(shù);
(2)請選用(1)中的一個函數(shù)關(guān)系式,說明如何設(shè)計,所用的鋼管材料最省?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】魚卷是泉州十大名小吃之一,不但本地人喜歡,而且深受外來游客的贊賞.小張從事魚卷生產(chǎn)和批發(fā)多年,有著不少來自零售商和酒店的客戶當(dāng)?shù)氐牧?xí)俗是農(nóng)歷正月不生產(chǎn)魚卷,客戶正月所需要的魚卷都會在上一年農(nóng)歷十二月底進行一次性采購小張把去年年底采購魚卷的數(shù)量x(單位:箱)在![]() 的客戶稱為“熟客”,并把他們?nèi)ツ瓴少彽臄?shù)量制成下表:
的客戶稱為“熟客”,并把他們?nèi)ツ瓴少彽臄?shù)量制成下表:
采購數(shù)x |
|
|
|
|
|
客戶數(shù) | 10 | 10 | 5 | 20 | 5 |
(1)根據(jù)表中的數(shù)據(jù)作出頻率分布直方圖,并估計采購數(shù)在168箱以上(含168箱)的“熟客”人數(shù);
(2)若去年年底“熟客”們采購的魚卷數(shù)量占小張去年年底總的銷售量的![]() ,估算小張去年年底總的銷售量(同一組中的數(shù)據(jù)用該組區(qū)間的中點值為代表);
,估算小張去年年底總的銷售量(同一組中的數(shù)據(jù)用該組區(qū)間的中點值為代表);
(3)由于魚卷受到游客們的青睞,小張做了一份市場調(diào)查,決定今年年底是否在網(wǎng)上出售魚卷,若不在網(wǎng)上出售魚卷,則按去年的價格出售,每箱利潤為20元,預(yù)計銷售量與去年持平;若在網(wǎng)上出售魚卷,則需把每箱售價下調(diào)2至5元,且每下調(diào)m元(![]() )銷售量可增加1000m箱,求小張今年年底收入Y(單位:元)的最大值.
)銷售量可增加1000m箱,求小張今年年底收入Y(單位:元)的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com