【題目】如圖，直棱柱
中，底面
是菱形，
，點F，Q是棱
，
的中點，
，
是棱
，
上的點，且
．
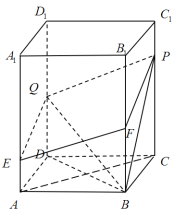
（1）求證：
平面
；
（2）求直線
與平面
所成角的正弦值．
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，
（1）討論
在
上的單調(diào)性.
（2）當
時，若在
上的最大值為
，討論：函數(shù)在
內(nèi)的零點個數(shù).
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在三棱柱ABC﹣A1B1C1中，E是棱AB的中點，動點F是側面ACC1A1（包括邊界）上一點，若EF//平面BCC1B1，則動點F的軌跡是（ ）
A.線段B.圓弧
C.橢圓的一部分D.拋物線的一部分
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在正方體
中，P，Q，M，N，H，R是各條棱的中點.
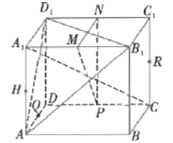
①直線
平面
；②
；③P，Q，H，R四點共面；④
平面
.其中正確的個數(shù)為（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在等腰梯形
中，
，
，
，E，F分別為
，
邊的中點.現(xiàn)將
沿著
折疊到
的位置，使得平面
平面
.
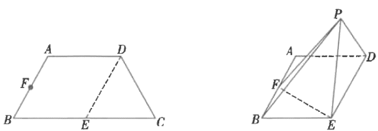
（1）證明：平面
平面
；
（2）求二面角
的余弦值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，
，且
與
的圖象有一條斜率為1的公切線（e為自然對數(shù)的底數(shù)）.
（1）求
；
（2）設函數(shù)
，證明：當
時，
有且僅有2個零點.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】2019年底，武漢發(fā)生“新型冠狀病毒”肺炎疫情，國家衛(wèi)健委緊急部署，從多省調(diào)派醫(yī)務工作者前去支援，正值農(nóng)歷春節(jié)舉家團圓之際，他們成為“最美逆行者”．武漢市從2月7日起舉全市之力入戶上門排查確診的新冠肺炎患者疑似的新冠肺炎患者無法明確排除新冠肺炎的發(fā)熱患者和確診患者的密切接觸者等“四類”人員，強化網(wǎng)格化管理，不落一戶不漏一人．若在排查期間，某小區(qū)有5人被確認為“確診患者的密切接觸者”，現(xiàn)醫(yī)護人員要對這5人隨機進行逐一“核糖核酸”檢測，只要出現(xiàn)一例陽性，則將該小區(qū)確定為“感染高危小區(qū)”．假設每人被確診的概率均為
且相互獨立，若當
時，至少檢測了4人該小區(qū)被確定為“感染高危小區(qū)”的概率取得最大值，則
____．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某市場研究人員為了了解產(chǎn)業(yè)園引進的甲公司前期的經(jīng)營狀況，對該公司2019年連續(xù)六個月的利潤進行了統(tǒng)計，并根據(jù)得到的數(shù)據(jù)繪制了相應的折線圖，如圖所示：
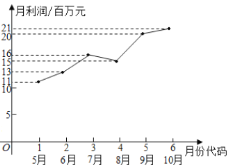
（1）由折線圖可以看出，可用線性回歸模型擬合月利潤
(單位：百萬元)與月份代碼
之間的關系，求關于的線性回歸方程，并預測該公司2020年4月份的利潤；
（2）甲公司新研制了一款產(chǎn)品，需要采購一批新型材料，現(xiàn)有A，B兩種型號的新型材料可供選擇，按規(guī)定每種新型材料最多可使用4個月，但新材料的不穩(wěn)定性會導致材料的使用壽命不同，現(xiàn)對A，B兩種型號的新型材料對應的產(chǎn)品各100件進行科學模擬測試，得到兩種新型材料使用壽命的頻數(shù)統(tǒng)計如下表：
經(jīng)甲公司測算平均每件新型材料每月可以帶來6萬元收人入，不考慮除采購成本之外的其他成本，A型號材料每件的采購成本為10萬元，B型號材料每件的采購成本為12萬元.假設每件新型材料的使用壽命都是整月數(shù)，且以頻率作為每件新型材料使用壽命的概率，如果你是甲公司的負責人，以每件新型材料產(chǎn)生利潤的平均值為決策依據(jù)，你會選擇采購哪款新型材料？
參考數(shù)據(jù)：
，
.
參考公式：回歸直線方程
，其中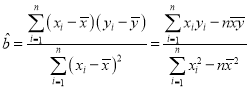
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
