【題目】已知
（1）求函數
的定義域;
（2）判斷函數的奇偶性，并予以證明。
【答案】（1）（-1，1）（2）奇函數
【解析】
（1）由題意可得f（x）﹣g（x）=loga（1+x）﹣loga（1﹣x）=
，由 
求得函數的定義域；
（2）由于f（x）﹣g（x）=，它的定義域為（﹣1，1），令h（x）=f（x）﹣g（x），可得h（﹣x）=﹣h（x），從而得到函數h（x）=f（x）﹣g（x）為奇函數．
（1）由于f（x）=loga（1+x），g（x）=loga（1﹣x），故f（x）﹣g（x）=loga（1+x）﹣loga（1﹣x）=，
由 ，求得﹣1＜x＜1，故函數的定義域為（﹣1，1）．
（2）由于f（x）﹣g（x）=loga（1+x）﹣loga（1﹣x）=，它的定義域為（﹣1，1），令h（x）=f（x）﹣g（x），
可得h（﹣x）=
=﹣=﹣h（x），故函數h（x）=f（x）﹣g（x）為奇函數．
科目：高中數學 來源： 題型：
【題目】某種新產品投放市場的100天中，前40天價格呈直線上升，而后60天其價格呈直線下降，現統計出其中4天的價格如下表：
時間 | 第4天 | 第32天 | 第60天 | 第90天 |
價格（千元） | 23 | 30 | 22 | 7 |
（1）寫出價格
關于時間
的函數關系式；（
表示投放市場的第
天）；
（2）銷售量
與時間的函數關系：
，則該產品投放市場第幾天銷售額最高？最高為多少千元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義域為{x|x≠0}的偶函數f（x），其導函數為f′（x），對任意正實數x滿足xf′（x）＞﹣2f（x），若g（x）=x2f（x），則不等式g（x）＜g（1﹣x）的解集是（ ）
A.（ 
，+∞）
B.（﹣∞， ）
C.（﹣∞，0）∪（0， ）
D.（0， ）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在半徑為R的圓桌上擺放同樣大小的半徑為r的硬幣.要求硬幣不準露出圓桌面邊緣，并且所擺硬幣彼此不能重疊.當擺放n枚硬幣之后，圓桌上就不能再多擺放一枚這種硬幣了.求證：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某糧庫擬建一個儲糧倉如圖所示，其下部是高為2的圓柱，上部是母線長為2的圓錐，現要設計其底面半徑和上部圓錐的高，若設圓錐的高
為
，儲糧倉的體積為
.
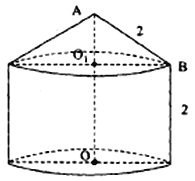
（1）求
關于
的函數關系式；（圓周率用
表示）
（2）求
為何值時，儲糧倉的體積最大.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，內角A，B，C對邊分別為a，b，c，且c＜a，已知 
=﹣2，tanB=2 
，b=3．
（1）求a和c的值；
（2）求sin（B﹣C）的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
