
【題目】在△ABC中,內(nèi)角A,B,C對邊分別為a,b,c,且c<a,已知 ![]() =﹣2,tanB=2
=﹣2,tanB=2 ![]() ,b=3.
,b=3.
(1)求a和c的值;
(2)求sin(B﹣C)的值.
【答案】
(1)解:∵ ![]() =﹣2,
=﹣2,
∴ ![]() =2,
=2,
∴cacosB=2,
∵tanB=2 ![]() ,
,
∴cosB= ![]() =
= ![]() ,
,
∴ac=2
在△ABC中,由余弦定理得:b2=a2+c2﹣2accosB,
即a2+c2=13,
∴a=2,c=3,或a=3,c=2,
∵a>c,
∴a=3,c=2
(2)解:在△ABC中,sinB=cosBtanB= ![]() ,
,
由正弦定理得sinC= ![]() =
= ![]()
![]() =
= ![]() ,
,
∵a=b>c,
∴C為銳角,
∴cosC= ![]() =
= ![]() ,
,
∴sin(B﹣C)=sinBcosC﹣cosBsinC= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]()
【解析】(1)由tanB=2 ![]() 得cosB,由知
得cosB,由知 ![]() ﹣2得accosB=2,解得ac,由余弦定理及a>c,即可解得a,c的值.(2)由(Ⅰ)可求sinB,由正弦定理可求sinC,cosC,利用兩角差的正弦函數(shù)公式即可得解.
﹣2得accosB=2,解得ac,由余弦定理及a>c,即可解得a,c的值.(2)由(Ⅰ)可求sinB,由正弦定理可求sinC,cosC,利用兩角差的正弦函數(shù)公式即可得解.


 口算能手系列答案
口算能手系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C: ![]() +
+ ![]() =1(α>b>0)的右焦點到直線x﹣y+3
=1(α>b>0)的右焦點到直線x﹣y+3 ![]() =0的距離為5,且橢圓的一個長軸端點與一個短軸端點間的距離為
=0的距離為5,且橢圓的一個長軸端點與一個短軸端點間的距離為 ![]() .
.
(1)求橢圓C的方程;
(2)在x軸上是否存在點Q,使得過Q的直線與橢圓C交于A、B兩點,且滿足 ![]() +
+ ![]() 為定值?若存在,請求出定值,并求出點Q的坐標(biāo);若不存在,請說明理由.
為定值?若存在,請求出定值,并求出點Q的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
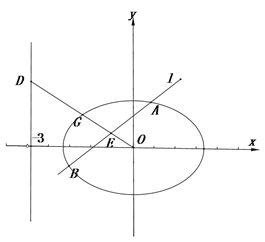
【題目】在平面直角坐標(biāo)系![]() 中,已知橢圓
中,已知橢圓![]() .如圖所示,斜率為
.如圖所示,斜率為![]() 且不過原點的直線
且不過原點的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,射線
,射線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,交直線
,交直線![]() 于點
于點![]() .
.
(Ⅰ)求![]() 的最小值;
的最小值;
(Ⅱ)若![]() ,
,
求證:直線![]() 過定點;
過定點;
(ii)試問點![]() 能否關(guān)于
能否關(guān)于![]() 軸對稱?若能,求出此時
軸對稱?若能,求出此時![]() 的外接圓方程;若不能,請說明理由.
的外接圓方程;若不能,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 的圖像與
的圖像與![]() 軸的交點為
軸的交點為![]() ,在
,在![]() 軸右側(cè)的第一個最高點和第一個與
軸右側(cè)的第一個最高點和第一個與![]() 軸交點分別為
軸交點分別為![]()
(1)求![]() 的解析式;
的解析式;
(2)將函數(shù)![]() 圖像上所有點的橫坐標(biāo)變?yōu)樵瓉淼?/span>
圖像上所有點的橫坐標(biāo)變?yōu)樵瓉淼?/span>![]() 倍(縱坐標(biāo)不變),再將所得圖像沿
倍(縱坐標(biāo)不變),再將所得圖像沿![]() 軸正方向平移
軸正方向平移![]() 個單位,得到函數(shù)
個單位,得到函數(shù)![]() 的圖像,求
的圖像,求![]() 的解析式;
的解析式;
(3)在(2)的條件下求函數(shù)![]() 在
在![]() 上的值域。
上的值域。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)業(yè)余足球運動員共有15000人,其中男運動員9000人,女運動員6000人,為調(diào)查該地區(qū)業(yè)余足球運動員每周平均踢足球占用時間的情況,采用分層抽樣的方法,收集300位業(yè)務(wù)足球運動員每周平均踢足球占用時間的樣本數(shù)據(jù)(單位:小時)
得到業(yè)余足球運動員每周平均踢足球所占用時間的頻率分布直方圖(如圖所示),其中樣本數(shù)據(jù)分組區(qū)間為:(0,2],(2,4],(4,6],(6,8],(8,10],(10,12].
將“業(yè)務(wù)運動員的每周平均踢足球時間所占用時間超過4小時”
定義為“熱愛足球”.
附:K2= ![]()
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
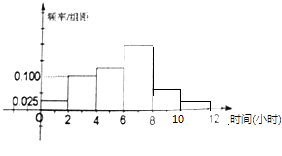
(1)應(yīng)收集多少位女運動員樣本數(shù)據(jù)?
(2)估計該地區(qū)每周平均踢足球所占用時間超過4個小時的概率.
(3)在樣本數(shù)據(jù)中,有80位女運動員“熱愛足球”.請畫出“熱愛足球與性別”列聯(lián)表,并判斷是否有99%的把握認為“熱愛足球與性別有關(guān)”.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為響應(yīng)十九大報告提出的實施鄉(xiāng)村振興戰(zhàn)略,某村莊投資![]() 萬元建起了一座綠色農(nóng)產(chǎn)品加工廠.經(jīng)營中,第一年支出
萬元建起了一座綠色農(nóng)產(chǎn)品加工廠.經(jīng)營中,第一年支出![]() 萬元,以后每年的支出比上一年增加了
萬元,以后每年的支出比上一年增加了![]() 萬元,從第一年起每年農(nóng)場品銷售收入為
萬元,從第一年起每年農(nóng)場品銷售收入為![]() 萬元(前
萬元(前![]() 年的純利潤綜合=前
年的純利潤綜合=前![]() 年的 總收入-前
年的 總收入-前![]() 年的總支出-投資額
年的總支出-投資額![]() 萬元).
萬元).
(1)該廠從第幾年開始盈利?
(2)該廠第幾年年平均純利潤達到最大?并求出年平均純利潤的最大值.
【答案】(1) 從第![]() 開始盈利(2) 該廠第
開始盈利(2) 該廠第![]() 年年平均純利潤達到最大,年平均純利潤最大值為
年年平均純利潤達到最大,年平均純利潤最大值為![]() 萬元
萬元
【解析】試題分析:(1)根據(jù)公式得到![]() ,令函數(shù)值大于0解得參數(shù)范圍;(2)根據(jù)公式得到
,令函數(shù)值大于0解得參數(shù)范圍;(2)根據(jù)公式得到![]() ,由均值不等式得到函數(shù)最值.
,由均值不等式得到函數(shù)最值.
解析:
由題意可知前![]() 年的純利潤總和
年的純利潤總和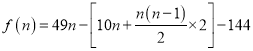
![]()
(1)由![]() ,即
,即![]() ,解得
,解得![]()
由![]() 知,從第
知,從第![]() 開始盈利.
開始盈利.
(2)年平均純利潤![]()
因為![]() ,即
,即![]()
所以![]()
當(dāng)且僅當(dāng)![]() ,即
,即![]() 時等號成立.
時等號成立.
年平均純利潤最大值為![]() 萬元,
萬元,
故該廠第![]() 年年平均純利潤達到最大,年平均純利潤最大值為
年年平均純利潤達到最大,年平均純利潤最大值為![]() 萬元.
萬元.
【題型】解答題
【結(jié)束】
21
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,并且滿足
,并且滿足![]() ,
, ![]() .
.
(1)求數(shù)列![]() 通項公式;
通項公式;
(2)設(shè)![]() 為數(shù)列
為數(shù)列![]() 的前
的前![]() 項和,求證:
項和,求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a>0,b>0,c>0,函數(shù)f(x)=|x﹣a|+|x+b|+c的最小值為1.
(1)求a+b+c的值;
(2)求證:a2+b2+c2 ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC為銳角三角形,命題p:不等式logcosC ![]() >0恒成立,命題q:不等式logcosC
>0恒成立,命題q:不等式logcosC ![]() >0恒成立,則復(fù)合命題p∨q、p∧q、¬p中,真命題的個數(shù)為( )
>0恒成立,則復(fù)合命題p∨q、p∧q、¬p中,真命題的個數(shù)為( )
A.0
B.1
C.2
D.3
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com