
【題目】隨著網絡營銷和電子商務的興起,人們的購物方式更具多樣化,某調查機構隨機抽取10名購物者進行采訪,5名男性購物者中有3名傾向于選擇網購,2名傾向于選擇實體店,5名女性購物者中有2名傾向于選擇網購,3名傾向于選擇實體店.
(1)若從10名購物者中隨機抽取2名,其中男、女各一名,求至少1名傾向于選擇實體店的概率;
(2)若從這10名購物者中隨機抽取3名,設X表示抽到傾向于選擇網購的男性購物者的人數,求X的分布列和數學期望.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知點
中,已知點![]() 為直線
為直線![]() 上一點,過點
上一點,過點![]() 作
作![]() 的垂線與以
的垂線與以![]() 為直徑的圓
為直徑的圓![]() 相交于
相交于![]() ,
,![]() 兩點.
兩點.
(1)若![]() ,求圓
,求圓![]() 的方程;
的方程;
(2)求證:點![]() 始終在某定圓上.
始終在某定圓上.
(3)是否存在一定點![]() (異于點
(異于點![]() ),使得
),使得![]() 為常數?若存在,求出定點
為常數?若存在,求出定點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cos(ωx+φ)(ω>0),f'(x)是f(x)的導函數,若f(α)=0,f'(α)>0,且f(x)在區間[α, ![]() +α)上沒有最小值,則ω取值范圍是( )
+α)上沒有最小值,則ω取值范圍是( )
A.(0,2)
B.(0,3]
C.(2,3]
D.(2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(14分)已知a,b為常數,且a≠0,函數f(x)=﹣ax+b+axlnx,f(e)=2(e=2.71828…是自然對數的底數).
(I)求實數b的值;
(II)求函數f(x)的單調區間;
(III)當a=1時,是否同時存在實數m和M(m<M),使得對每一個t∈[m,M],直線y=t與曲線y=f(x)(x∈[![]() ,e])都有公共點?若存在,求出最小的實數m和最大的實數M;若不存在,說明理由.
,e])都有公共點?若存在,求出最小的實數m和最大的實數M;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}滿足an>1,其前n項和Sn滿足6Sn=an2+3an+2
(1)求數列{an}的通項公式及前n項和Sn;
(2)設數列{bn}滿足bn= ![]() ,且其前n項和為Tn , 證明:
,且其前n項和為Tn , 證明: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為 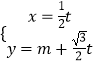 (t為參數),以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,曲線C的極坐標方程為ρ2﹣2ρcosθ﹣4=0
(t為參數),以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,曲線C的極坐標方程為ρ2﹣2ρcosθ﹣4=0
(1)若直線l與曲線C沒有公共點,求m的取值范圍;
(2)若m=0,求直線l被曲線C截得的弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據統計,某地區植被覆蓋面積![]() 公頃
公頃![]() 與當地氣溫下降的度數
與當地氣溫下降的度數![]() 之間呈線性相關關系,對應數據如下:
之間呈線性相關關系,對應數據如下:
| 20 | 40 | 60 | 80 |
| 3 | 4 | 4 | 5 |
![]() 請用最小二乘法求出y關于x的線性回歸方程;
請用最小二乘法求出y關于x的線性回歸方程;
![]() 根據
根據![]() 中所求線性回歸方程,如果植被覆蓋面積為300公頃,那么下降的氣溫大約是多少
中所求線性回歸方程,如果植被覆蓋面積為300公頃,那么下降的氣溫大約是多少![]() ?
?
參考公式:線性回歸方程![]() ;其中
;其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了更好地了解鯨的生活習性,某動物保護組織在受傷的鯨身上安裝了電子監測設備,從海岸線放歸點![]() 處把它放歸大海,并沿海岸線由西到東不停地對其進行跟蹤觀測。在放歸點
處把它放歸大海,并沿海岸線由西到東不停地對其進行跟蹤觀測。在放歸點![]() 的正東方向有一觀測站
的正東方向有一觀測站![]() ,可以對鯨進行生活習性的詳細觀測。已知
,可以對鯨進行生活習性的詳細觀測。已知![]() ,觀測站
,觀測站![]() 的觀測半徑為
的觀測半徑為![]() .現以點
.現以點![]() 為坐標原點、以由西向東的海岸線所在直線為
為坐標原點、以由西向東的海岸線所在直線為![]() 軸建立平面直角坐標系,則可以測得鯨的行進路線近似的滿足
軸建立平面直角坐標系,則可以測得鯨的行進路線近似的滿足![]() .
.

(1)若測得鯨的行進路線上一點![]() ,求
,求![]() 的值;
的值;
(2)在(1)問的條件下,問:
①當鯨運動到何處時,開始進入觀測站![]() 的觀測區域內?(計算結果精確到0.1)
的觀測區域內?(計算結果精確到0.1)
②當鯨運動到何處時,離觀測站![]() 距離最近(觀測最便利)?(計算結果精確到0.1)
距離最近(觀測最便利)?(計算結果精確到0.1)
(參考數據:![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=cos(x+ ![]() ),則下列結論錯誤的是( )
),則下列結論錯誤的是( )
A.f(x)的一個周期為﹣2π
B.y=f(x)的圖象關于直線x= ![]() 對稱
對稱
C.f(x+π)的一個零點為x= ![]()
D.f(x)在( ![]() ,π)單調遞減
,π)單調遞減
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com