
【題目】為了解甲、乙兩個快遞公司的工作狀況,假設同一個公司快遞員的工作狀況基本相同,現從甲、乙兩公司各隨機抽取一名快遞員,并從兩人某月(30天)的快遞件數記錄結果中隨機抽取10天的數據,制表如下:

每名快遞員完成一件貨物投遞可獲得的勞務費情況如下:
甲公司規定每件4.5元;乙公司規定每天35件以內(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根據表中數據寫出甲公司員工![]() 在這10天投遞的快遞件數的平均數和眾數;
在這10天投遞的快遞件數的平均數和眾數;
(2)為了解乙公司員工![]() 的每天所得勞務費的情況,從這10天中隨機抽取1天,他所得的勞務費記為
的每天所得勞務費的情況,從這10天中隨機抽取1天,他所得的勞務費記為![]() (單位:元),求
(單位:元),求![]() 的概率;
的概率;
(3)根據表中數據估算公司的每位員工在該月所得的勞務費.
【答案】(1)平均數為36,眾數為33;(2)![]() ;(3)4965元.
;(3)4965元.
【解析】試題分析:(1)由莖葉圖能求出甲公司員工![]() 投遞快遞件數的平均數和眾數;(2)由題意能求出
投遞快遞件數的平均數和眾數;(2)由題意能求出![]() 時,
時, ![]() 的可能取值為44,42,42,42,即可求出相對應的概率;(3)由(2)可知勞務費
的可能取值為44,42,42,42,即可求出相對應的概率;(3)由(2)可知勞務費![]() 可能的取值為136,147,154,189,203,結合表中數據,即可得估算公司的每位員工在該月所得的勞務費.
可能的取值為136,147,154,189,203,結合表中數據,即可得估算公司的每位員工在該月所得的勞務費.
試題解析:(1)甲公司員工![]() 投遞快遞件數的平均數為36,眾數為33;
投遞快遞件數的平均數為36,眾數為33;
(2)設![]() 為乙公司員工
為乙公司員工![]() 投遞件數,則
投遞件數,則
![]() 時,
時, ![]() 元,當
元,當![]() 時,
時, ![]() 元,
元,
令![]() ,得
,得![]() ,則
,則![]() 取值為44,42,42,42,
取值為44,42,42,42,
所以![]() 的概率為
的概率為![]() ;
;
(3)根據表中數據,可估算甲公司的員工該月收入為![]() 元,由(2)可知勞務費
元,由(2)可知勞務費![]() 可能的取值為136,147,154,189,203,
可能的取值為136,147,154,189,203,
∴乙公司的員工該月收入為![]() 元.
元.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】經過市場調查,超市中的某種小商品在過去的近40天的日銷售量(單位:件)與價格(單位:元)為時間![]() (單位:天)的函數,且日銷售量近似滿足
(單位:天)的函數,且日銷售量近似滿足![]() ,價格近似滿足
,價格近似滿足![]() 。
。
(1)寫出該商品的日銷售額![]() (單位:元)與時間
(單位:元)與時間![]() (
(![]() )的函數解析式并用分段函數形式表示該解析式(日銷售額=銷售量
)的函數解析式并用分段函數形式表示該解析式(日銷售額=銷售量![]() 商品價格);
商品價格);
(2)求該種商品的日銷售額![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了紀念五四運動100周年和建團97周年,某校團委開展“青春心向黨,建功新時代”知識問答競賽.在小組賽中,甲乙丙3人進行擂臺賽,每局2人進行比賽,另1人當裁判,每一局的輸方擔任下局的裁判,由原來裁判向勝者挑戰,甲乙丙3人實力相當.
(1)若第1局是由甲擔任裁判,求第4局仍是甲擔任裁判的概率;
(2)甲乙丙3人進行的擂臺賽結束后,經統計,甲共參賽了6局,乙共參賽了5局而丙共擔任了2局裁判.則甲乙丙3人進行的擂臺賽共進行了多少局?若從小組賽中,甲乙丙比賽的所有場次中任取2場,則均是由甲擔任裁判的概率是多少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農科所對冬季晝夜溫差大小與某反季節大豆新品種發芽多少之間的關系進行分析研究,他們分別記錄了12月1日至12月5日的每天晝夜溫差與實驗室每天每100顆種子中的發芽數,得到如下資料:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
溫差 | 10 | 11 | 13 | 12 | 8 |
發芽數 | 23 | 25 | 30 | 26 | 16 |
該農科所確定的研究方案是:先從這5組數據中選取2組,用剩下的3組數據求線性回歸方程,再用被選取的2組數據進行檢驗.
(1)求選取的2組數據恰好是不相鄰2天的數據的概率;
(2)若選取的是12月1日與12月5日的2組數據,請根據12月2日至4日的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,由線性回歸方程得到的估計數據與所選取的檢驗數據的誤差均不超過2顆,則認為得到的線性回歸方程是可靠的,試問(2)中所得的線性回歸方程是否可靠?
,由線性回歸方程得到的估計數據與所選取的檢驗數據的誤差均不超過2顆,則認為得到的線性回歸方程是可靠的,試問(2)中所得的線性回歸方程是否可靠?
附:參考公式: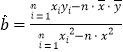 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年空氣質量逐步惡化,霧霾天氣現象出現增多,大氣污染危害加重. 大氣污染可引起心悸、呼吸困難等心肺疾病。為了解某市心肺疾病是否與性別有關,在某醫院隨機的對入院50人進行了問卷調查得到了如在的列聯表:已知在全部50人中隨機抽取1人,抽到患心肺疾病的人的概率為![]() .
.
(Ⅰ)請將右面的列聯表補充完整;
患心肺疾病 | 不患心肺疾病 | 合計 | |
男 | 5 | ||
女 | 10 | ||
合計 | 50 |
(Ⅱ)是否有99.5%的把握認為患心肺疾病與性別有關?說明你的理由;
(Ⅲ)已知在患心肺疾病的10位女性中,有3位又患胃病.現在從患心肺疾病的10位女性中,選出3名進行其他方面的排查,記選出患胃病的女性人數為![]() ,求
,求![]() 的分布列以及數學期望.
的分布列以及數學期望.
下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式![]() 其中
其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某漁輪在航行中不幸遇險,發出呼救信號,我海軍艦艇在A處獲悉后,立即測出該漁輪在方位角為45°,距離為10mile的C處,并測得漁輪正沿方位角為105°的方向,以![]() mile/h的速度向某小島靠攏,我海軍艦艇立即向方位角為
mile/h的速度向某小島靠攏,我海軍艦艇立即向方位角為![]() 方向,以
方向,以![]() mile/h的速度前去營救,求艦艇與漁輪相遇時所需的最短時間和
mile/h的速度前去營救,求艦艇與漁輪相遇時所需的最短時間和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】判斷下列命題的真假:
(1)存在兩個無理數,它們的乘積是有理數;
(2)如果實數集的子集A是有限集,則A中的元素一定有最大值;
(3)沒有一個無理數不是實數;
(4)如果一個四邊形的對角線相等,則這個四邊形是矩形;
(5)集合A是集合![]() 的子集;
的子集;
(6)集合![]() 是集合A的子集.
是集合A的子集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com