
【題目】已知曲線![]() ,問是否存在實數(shù)a,使得經(jīng)過點(1,a)能夠作出該曲線的兩條切線?若存在求出實數(shù)a的取值范圍,若不存在,說明理由.
,問是否存在實數(shù)a,使得經(jīng)過點(1,a)能夠作出該曲線的兩條切線?若存在求出實數(shù)a的取值范圍,若不存在,說明理由.
 ABC考王全優(yōu)卷系列答案
ABC考王全優(yōu)卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】對某校高一年級學生參加社區(qū)服務次數(shù)進行統(tǒng)計,隨機抽取![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區(qū)服務的次數(shù).根據(jù)此數(shù)據(jù)作出了頻數(shù)與頻率的統(tǒng)計表和頻率分布直方圖如下:
名學生參加社區(qū)服務的次數(shù).根據(jù)此數(shù)據(jù)作出了頻數(shù)與頻率的統(tǒng)計表和頻率分布直方圖如下:
分組 | 頻數(shù) | 頻率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合計 |
| 1 |

(1)求出表中![]() 及圖中
及圖中![]() 的值;
的值;
(2)試估計他們參加社區(qū)服務的平均次數(shù);
(3)在所取樣本中,從參加社區(qū)服務的次數(shù)不少于20次的學生中任選2人,求至少1人參加社區(qū)服務次數(shù)在區(qū)間![]() 內(nèi)的概率.
內(nèi)的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() R,命題
R,命題![]() :對任意
:對任意![]() ,不等式
,不等式![]() 恒成立;命題
恒成立;命題![]() :存在
:存在![]() ,使得
,使得![]() 成立.
成立.
(1)若![]() 為真命題,求
為真命題,求![]() 的取值范圍;
的取值范圍;
(2)若![]() 且
且![]() 為假,
為假, ![]() 或
或![]() 為真,求
為真,求![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示的程序框圖表示的算法功能是( )
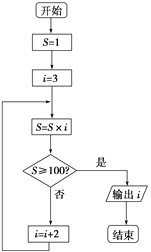
A. 計算小于100的奇數(shù)的連乘積
B. 計算從1開始的連續(xù)奇數(shù)的連乘積
C. 從1開始的連續(xù)奇數(shù)的連乘積,當乘積大于或等于100時,計算奇數(shù)的個數(shù)
D. 計算1×3×5×…×n≥100時的最小的n的值
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}的首項a1=a,其前n項和為Sn , 且滿足Sn+Sn﹣1=3n2+2n+4(n≥2),若對任意的n∈N* , an<an+1恒成立,則a的取值范圍是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】 【2016高考新課標Ⅲ文數(shù)】已知拋物線![]() :
:![]() 的焦點為
的焦點為![]() ,平行于
,平行于![]() 軸的兩條直線
軸的兩條直線![]() 分別交
分別交![]() 于
于![]() 兩點,交
兩點,交![]() 的準線于
的準線于![]() 兩點.
兩點.
(I)若![]() 在線段
在線段![]() 上,
上,![]() 是
是![]() 的中點,證明
的中點,證明![]() ;
;
(II)若![]() 的面積是
的面積是![]() 的面積的兩倍,求
的面積的兩倍,求![]() 中點的軌跡方程.
中點的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】【2016高考山東文數(shù)】已知橢圓C:![]() (a>b>0)的長軸長為4,焦距為2
(a>b>0)的長軸長為4,焦距為2![]() .
.
(I)求橢圓C的方程;
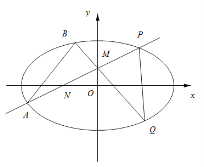
(Ⅱ)過動點M(0,m)(m>0)的直線交x軸與點N,交C于點A,P(P在第一象限),且M是線段PN的中點.過點P作x軸的垂線交C于另一點Q,延長線QM交C于點B.
(i)設直線PM、QM的斜率分別為k、k',證明![]() 為定值.
為定值.
(ii)求直線AB的斜率的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】【2016高考天津文數(shù)】某化肥廠生產(chǎn)甲、乙兩種混合肥料,需要A,B,C三種主要原料.生產(chǎn)1車皮甲種肥料和生產(chǎn)1車皮乙種肥料所需三種原料的噸數(shù)如下表所示:
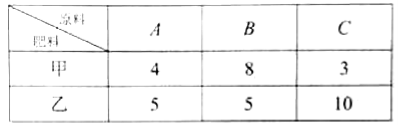
現(xiàn)有A種原料200噸,B種原料360噸,C種原料300噸,在此基礎上生產(chǎn)甲、乙兩種肥料.已知生產(chǎn)1車皮甲種肥料,產(chǎn)生的利潤為2萬元;生產(chǎn)1車皮乙種肥料,產(chǎn)生的利潤為3萬元.分別用x,y計劃表示生產(chǎn)甲、乙兩種肥料的車皮數(shù).
(Ⅰ)用x,y列出滿足生產(chǎn)條件的數(shù)學關(guān)系式,并畫出相應的平面區(qū)域;
(Ⅱ)問分別生產(chǎn)甲、乙兩種肥料各多少車皮,能夠產(chǎn)生最大的利潤?并求出此最大利潤.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=sin(ωx+φ)(其中ω>0|φ|< ![]() )圖象相鄰對稱軸的距離為
)圖象相鄰對稱軸的距離為 ![]() ,一個對稱中心為(﹣
,一個對稱中心為(﹣ ![]() ,0),為了得到g(x)=cosωx的圖象,則只要將f(x)的圖象( )
,0),為了得到g(x)=cosωx的圖象,則只要將f(x)的圖象( )
A.向右平移 ![]() 個單位
個單位
B.向右平移 ![]() 個單位
個單位
C.向左平移 ![]() 個單位
個單位
D.向左平移 ![]() 個單位
個單位
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com