
【題目】已知函數![]() (
(![]() ).
).
(1)若曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 平行,求
平行,求![]() 的值;
的值;
(2)若對于任意![]() 且
且![]() ,都有
,都有![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
(3)若對于任意![]() ,都有
,都有![]() 成立,求整數
成立,求整數![]() 的最大值.
的最大值.
(其中![]() 為自然對數的底數)
為自然對數的底數)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)由題意得:![]() ,由題意可得
,由題意可得![]() ,解得
,解得![]() .
.
(2)因為![]() ,所以
,所以![]() ,
,
記![]() ,可知
,可知![]() 在
在![]() 上單調遞增.
上單調遞增.
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,記
上恒成立,記![]() ,即可求得
,即可求得![]() 的取值范圍.
的取值范圍.
(3)若對于任意![]() ,都有
,都有![]() 成立,
成立,
所以![]() 對于任意
對于任意![]() 恒成立,
恒成立,
即![]() 對于任意
對于任意![]() 恒成立,
恒成立,
令![]() ,利用導數研究函數
,利用導數研究函數![]() 的性質,即可得到整數
的性質,即可得到整數![]() 的最大值.
的最大值.
詳解:
(1)由題意得:![]() ,
,
又曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 平行,
平行,
所以![]() ,解得
,解得![]() .
.
(2)因為![]() ,所以
,所以![]() ,
,
記![]() ,又因為
,又因為![]() 且
且![]() ,
,
所以![]() 在
在![]() 上單調遞增.
上單調遞增.
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,記
上恒成立,記![]() ,
,
所以![]() ,令
,令![]() ,解得
,解得![]() ,
,
因為當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
所以當![]() 時,
時,![]() 取到最大值
取到最大值![]() ,
,
所以![]() .
.
(3)若對于任意![]() ,都有
,都有![]() 成立,
成立,
所以![]() 對于任意
對于任意![]() 恒成立,
恒成立,
即![]() 對于任意
對于任意![]() 恒成立,
恒成立,
令![]() ,所以
,所以![]() ,
,
再令![]() ,所以
,所以![]() 在
在![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,
,![]() ,
,
所以必存在唯一的解![]() ,使得
,使得![]() ,
,
即![]() ,
,
所以當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
所以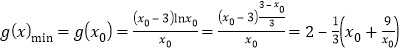 ,
,
因為![]() ,所以
,所以![]() ,
,
又因為![]() ,所以
,所以![]() 的最大整數為
的最大整數為![]() ,
,
所以整數![]() 的最大值為
的最大值為![]() .
.


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,圓C的參數方程為 ![]() (θ為參數),以O為極點,x軸的非負半軸為極軸且取相同的單位長度建立極坐標系.
(θ為參數),以O為極點,x軸的非負半軸為極軸且取相同的單位長度建立極坐標系.
(1)求圓C的極坐標方程;
(2)若直線l的極坐標方程是 ![]() ,射線
,射線 ![]() 與圓C的交點為O、P,與直線l的交點為Q.求線段PQ的長.
與圓C的交點為O、P,與直線l的交點為Q.求線段PQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某項“過關游戲”規則規定:在地![]() 關要拋擲
關要拋擲![]() 顆骰子
顆骰子![]() 次,如果這
次,如果這![]() 次拋擲所出現的點數和大于
次拋擲所出現的點數和大于![]() ,則算過關.
,則算過關.
(Ⅰ)此游戲最多能過__________關.
(Ⅱ)連續通過第![]() 關、第
關、第![]() 關的概率是__________.
關的概率是__________.
(Ⅲ)若直接挑戰第![]() 關,則通關的概率是__________.
關,則通關的概率是__________.
(Ⅳ)若直接挑戰第![]() 關,則通關的概率是__________.
關,則通關的概率是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() (
( ![]() ),若函數F(x)=f(x)﹣3的所有零點依次記為x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 則x1+2x2+2x3+…+2xn﹣1+xn= .
),若函數F(x)=f(x)﹣3的所有零點依次記為x1 , x2 , x3 , …,xn , 且x1<x2<x3<…<xn , 則x1+2x2+2x3+…+2xn﹣1+xn= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭記錄了未使用節水龍頭50天的日用水量數據(單位:m3)和使用了節水龍頭50天的日用水量數據,得到頻數分布表如下:
未使用節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
|
頻數 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
頻數 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答題卡上作出使用了節水龍頭50天的日用水量數據的頻率分布直方圖:
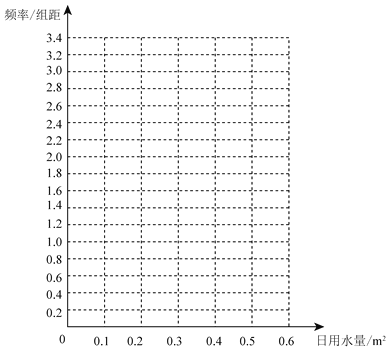
(2)估計該家庭使用節水龍頭后,日用水量小于0.35 m3的概率;
(3)估計該家庭使用節水龍頭后,一年能節省多少水?(一年按365天計算,同一組中的數據以這組數據所在區間中點的值作代表.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,甲、乙兩個企業的用電負荷量![]() 關于投產持續時間
關于投產持續時間![]() (單位:小時)的關系
(單位:小時)的關系![]() 均近似地滿足函數
均近似地滿足函數![]()
![]() .
.
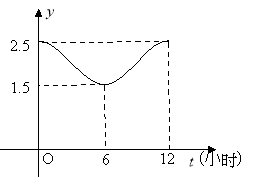
(1)根據圖象,求函數![]() 的解析式;
的解析式;
(2)為使任意時刻兩企業用電負荷量之和不超過![]() ,現采用錯峰用電的方式,讓企業乙比企業甲推遲
,現采用錯峰用電的方式,讓企業乙比企業甲推遲![]()
![]() 小時投產,求
小時投產,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
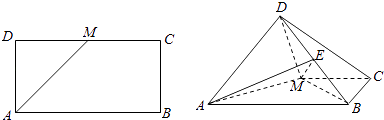
【題目】如圖,已知長方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M為DC的中點,將△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求證:AD⊥BM
,M為DC的中點,將△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求證:AD⊥BM
(Ⅱ)若點E是線段DB上的一動點,問點E在何位置時,二面角E﹣AM﹣D的余弦值為 ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com