Question

【題目】如圖，在四棱錐PABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP＝AB＝2，BC＝2，E，F分別是AD，PC的中點．

(1)證明：PC⊥平面BEF；

(2)求平面BEF與平面BAP夾角的大小．

Answer 1

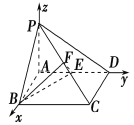
【答案】（1）見解析（2）45°.

【解析】

試題分析：本題主要以四棱錐為幾何背景考查線線垂直、線面垂直、二面角、向量法、向量垂直的充要條件等基礎(chǔ)知識，考查學生的空間想象能力、邏輯推理能力、計算能力.第一問，利用已知的垂直關(guān)系建立空間直角坐標系，得到點的坐標，從而得到相關(guān)向量的坐標，利用向量的數(shù)量積為0，證明兩直線垂直，再利用線面垂直的判定得到PC⊥平面BEF；第二問，平面BEF與平面BAP的法向量分別為和，利用夾角公式求夾角的余弦，從而確定角的值.

試題解析：(1)證明:如圖，

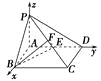
以A為坐標原點，AB，AD，AP所在直線分別為x，y，z軸建立空間直角坐標系．

∵AP＝AB＝2，BC＝AD＝，四邊形ABCD是矩形，

∴A，B，C，D，P的坐標為A(0,0,0)，B(2,0,0)，C(2,，0)，D(0,，0)，P(0,0,2)．

又E，F分別是AD，PC的中點，∴E(0，，0)，F(1，，1)．

∴＝(2,，－2)，＝(－1，，1)，＝(1,0,1)．

∴＝－2＋4－2＝0，＝2＋0－2＝0.

∴，

∴PC⊥BF，PC⊥EF.又BF∩EF＝F，

∴PC⊥平面BEF.

(2)由(1)知平面BEF的一個法向量n1＝＝(2,，－2)，平面BAP的一個法向量n2＝＝(0,，0)，

∴n1·n2＝8.

設(shè)平面BEF與平面BAP的夾角為θ，

則，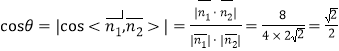

∴θ＝45°.∴平面BEF與平面BAP的夾角為45°.