
【題目】設函數![]()
![]() .
.
(1)求![]() 的單調區間;
的單調區間;
(2)當![]() 時,若對
時,若對![]() ,都有
,都有![]() (
(![]() )成立,求
)成立,求![]() 的最大值.
的最大值.
【答案】(1)答案不唯一,具體見解析(2)0
【解析】
(1)![]() ,
,![]() .對
.對![]() 分類討論,可得其單調區間.
分類討論,可得其單調區間.
(2)當![]() 時,對
時,對![]() ,都有
,都有![]() 恒成立,
恒成立, ![]() ,令
,令![]() ,只需
,只需![]() ,利用導數研究其單調性即可得出.
,利用導數研究其單調性即可得出.
解:(1)![]() ,
,![]()
![]() .
.
當![]() 時,
時,![]() 在
在![]() 恒成立,
恒成立,![]() 在
在![]() 是單減函數.
是單減函數.
當![]() 時,令
時,令![]() ,解之得
,解之得![]() .
.
從而,當![]() 變化時,
變化時,![]() ,
,![]() 隨
隨![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
| - | 0 | + |
| 單調遞減 | 單調遞增 |
由上表中可知,![]() 在
在![]() 是單減函數,在
是單減函數,在![]() 是單增函數.
是單增函數.
綜上,當![]() 時,
時,![]() 的單減區間為
的單減區間為![]() ;
;
當![]() 時,
時,![]() 的單減區間為
的單減區間為![]() ,單增區間為
,單增區間為![]() .
.
(2)當![]() ,
,![]() 為整數,且當
為整數,且當![]() 時,
時,![]() 恒成立
恒成立
![]() .
.
令![]() ,只需
,只需![]() ;
;
又![]() ,
,
由(1)得![]() 在
在![]() 單調遞增,且
單調遞增,且![]() ,
,
所以存在唯一的![]() ,使得
,使得![]() ,
,
當![]() ,即
,即![]() 單調遞減,
單調遞減,
當![]() ,即
,即![]() 單調遞增,
單調遞增,
所以![]() 時,
時,![]() 取得極小值,也是最小值,當
取得極小值,也是最小值,當![]() 時,
時,![]()
![]()
而![]() 在
在![]() 為增函數,
為增函數,![]()
![]() ,
,
即![]() .而
.而![]()
![]() ,
,
![]()
![]()
![]() ,
,![]() 即所求
即所求![]() 的最大值為0.
的最大值為0.


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案科目:高中數學 來源: 題型:
【題目】在一次籃球投籃測試中,記分規則如下(滿分為![]() 分):①每人可投籃
分):①每人可投籃![]() 次,每投中一次記
次,每投中一次記![]() 分;②若連續兩次投中加
分;②若連續兩次投中加![]() 分,連續三次投中加
分,連續三次投中加![]() 分,連續四次投中加
分,連續四次投中加![]() 分,以此類推,…,七次都投中加
分,以此類推,…,七次都投中加![]() 分.假設某同學每次投中的概率為
分.假設某同學每次投中的概率為![]() ,各次投籃相互獨立,則:(1)該同學在測試中得
,各次投籃相互獨立,則:(1)該同學在測試中得![]() 分的概率為______;(2)該同學在測試中得
分的概率為______;(2)該同學在測試中得![]() 分的概率為______..
分的概率為______..
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知球![]() 是正三棱錐(底面為正三角形,頂點在底面的射影為底面中心)
是正三棱錐(底面為正三角形,頂點在底面的射影為底面中心)![]() 的外接球,
的外接球,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() ,過點
,過點![]() 作球
作球![]() 的截面,則所得截面圓面積的取值范圍是( )
的截面,則所得截面圓面積的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在幾何體ABCDE中,四邊形ABCD是矩形,AB![]() 平面BEC,BE
平面BEC,BE![]() EC,AB=BE=EC=2,G,F分別是線段BE,DC的中點.
EC,AB=BE=EC=2,G,F分別是線段BE,DC的中點.
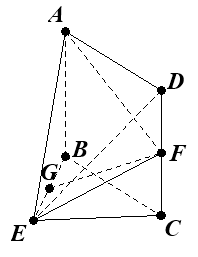
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求平面AEF與平面BEC所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)若不過原點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,與直線
兩點,與直線![]() 相交于點
相交于點![]() ,且
,且![]() 是線段
是線段![]() 的中點,求
的中點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從8名教師中選派4名同時去4個邊遠地區支教(每地1名教師),其中甲和乙不能都去,甲和丙只能都去或都不去,則不同的選派方案有( )
A.900種B.600種C.300種D.150種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲地到乙地要經過3個十字路口,設各路口信號燈工作相互獨立,且在各路口遇到紅燈的概率分別為![]() .
.
(Ⅰ)設![]() 表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量
表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)若有2輛車獨立地從甲地到乙地,求這2輛車共遇到1個紅燈的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題正確的是( )
①線性相關系數![]() 越大,兩個變量的線性相關性越強;反之,線性相關性越弱;
越大,兩個變量的線性相關性越強;反之,線性相關性越弱;
②殘差平方和越小的模型,擬合的效果越好;
③用相關指數![]() 來刻畫回歸效果,
來刻畫回歸效果,![]() 越小,說明模型的擬合的效果越好;
越小,說明模型的擬合的效果越好;
④隨機誤差![]() 是衡量預報精確度的一個量,它滿足
是衡量預報精確度的一個量,它滿足![]() .
.
A.①③B.①④C.②③D.②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com