
【題目】由數列![]() 中的項構成新數列
中的項構成新數列![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…是首項為1,公比為
,…是首項為1,公比為![]() 的等比數列.
的等比數列.
(1)數列![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】試題分析:(1)因為新數列a1,(a2-a1),(a3-a2),…,(an-an-1),…,此數列是首項為1,公比為![]() 的等比數列,根據等比數列的通項公式可得數列{an}的通項;
的等比數列,根據等比數列的通項公式可得數列{an}的通項;
(2)通過分組分別求等差數列的和以及錯位相減求和公式得到即可.
試題解析:(1)由題意知當![]() 時,
時,![]() ,
,
所以![]() ,
,
…
![]() ,
,
![]() ,
,
![]() 個式子累加得:
個式子累加得:
![]()
 ,
,
所以![]() .
.
(2)由(1)得![]() ,
,
設![]() ,
,![]() 分別為數列
分別為數列![]() ,
,![]() 的前
的前![]() 項和,
項和,
則![]() ,
,
![]() ,
,
所以![]() ,
,
兩式作差得:![]()

![]() .
.
所以![]() ,
,
所以![]() .
.
點晴:本題考查的是求數列通項和數列求和問題。觀察所給定數列的特征,新數列a1,(a2-a1),(a3-a2),…,(an-an-1),…,是首項為1,公比為![]() 的等比數列,根據等比數列的通項公式可得數列{an}的通項,從第二問的通項判斷需要分組求和. 通過分組分別求等差數列的和以及錯位相減求和公式得到即可.
的等比數列,根據等比數列的通項公式可得數列{an}的通項,從第二問的通項判斷需要分組求和. 通過分組分別求等差數列的和以及錯位相減求和公式得到即可.


科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.二進制數11010(2)化為八進制數為42(8)
B.若扇形圓心角為2弧度,且扇形弧所對的弦長為2,則這個扇形的面積為 ![]()
C.用秦九韶算法計算多項式f(x)=3x6+5x4+6x3﹣4x﹣5當x=3時的值時,v1=3v0+5=32
D.正切函數在定義域內為單調增函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機抽取某中學甲、乙兩班各10名同學,測量他們的身高(單位:cm),獲得身高數據的莖葉圖如圖7.

(1)根據莖葉圖判斷哪個班的平均身高較高;
(2)計算甲班的樣本方差;
(3)現從乙班這10名同學中隨機抽取兩名身高不低于173cm的同學,求身高為176cm的同學被抽中的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
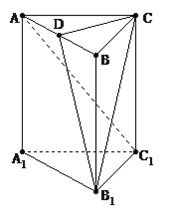
【題目】如圖,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC, 點D是AB的中點.
(Ⅰ)求證:CD⊥平面A1ABB1;
(Ⅱ)求證:AC1∥平面CDB1;
(Ⅲ)線段AB上是否存在點M,使得A1M⊥平面CDB1?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 與圓
與圓![]() :
: ![]() 相切,且與圓
相切,且與圓![]() :
: ![]() 相內切,記圓心
相內切,記圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .設
.設![]() 為曲線
為曲線![]() 上的一個不在
上的一個不在![]() 軸上的動點,
軸上的動點, ![]() 為坐標原點,過點
為坐標原點,過點![]() 作
作![]() 的平行線交曲線
的平行線交曲線![]() 于
于![]() ,
, ![]() 兩個不同的點.
兩個不同的點.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)試探究![]() 和
和![]() 的比值能否為一個常數?若能,求出這個常數,若不能,請說明理由;
的比值能否為一個常數?若能,求出這個常數,若不能,請說明理由;
(Ⅲ)記![]() 的面積為
的面積為![]() ,
, ![]() 的面積為
的面積為![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四邊形ABCD中,已知AB=9,BC=6, ![]() =2
=2 ![]() .
.
(1)若四邊形ABCD是矩形,求 ![]()
![]() 的值;
的值;
(2)若四邊形ABCD是平行四邊形,且 ![]()
![]() =6,求
=6,求 ![]() 與
與 ![]() 夾角的余弦值.
夾角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某地區學生和包括老師、家長在內的社會人士對高考英語改革的看法,某媒體在該地區選擇了3600人調查,就是否“取消英語聽力”的問題,調查統計的結果如下表:
![]()
| 應該取消 | 應該保留 | 無所謂 | |
在校學生 | 2100人 | 120人 | y人 | |
社會人士 | 600人 | x人 | z人 |
已知在全體樣本中隨機抽取1人,抽到持“應該保留”態度的人的概率為0.05.
(1)現用分層抽樣的方法在所有參與調查的人中抽取360人進行問卷訪談,問應在持“無所謂”態度的人中抽取多少人?
(2)在持“應該保留”態度的人中,用分層抽樣的方法抽取6人平均分成兩組進行深入交流,求第一組中在校學生人數ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
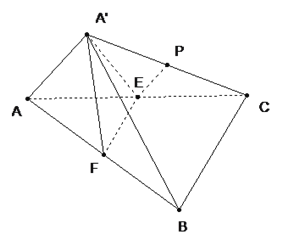
【題目】如圖, ![]() 、
、![]() 分別為直角三角形
分別為直角三角形![]() 的直角邊
的直角邊![]() 和斜邊
和斜邊![]() 的中點,沿
的中點,沿![]() 將
將![]() 折起到
折起到![]() 的位置,連結
的位置,連結![]() 、
、![]() ,
, ![]() 為
為![]() 的中點.
的中點.
(1)求證: ![]() 平面
平面![]() ;(2)求證:平面
;(2)求證:平面![]() 平面
平面![]() ;
;
(3)求證: ![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com