
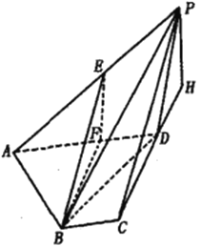
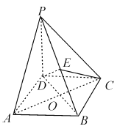
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]()
![]() 是等邊三角形,E是PA的中點,
是等邊三角形,E是PA的中點,![]() .
.

(1)求證:![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
【答案】(1)證明見解析;(2)3.
【解析】
(1)取AD中點F,連接BF,EF,結合已知證得AD⊥EF,又△ABC是正三角形,得AD⊥BF,由線面垂直的判定可得AD⊥平面BEF,進一步得到AD⊥BE;
(2)由AD∥BC,∠BCD=90°,得AD⊥CD,再由AD⊥PD,得AD⊥平面PCD,可得平面ABCD⊥平面PCD,過點P作PH⊥CD,交CD的延長線于點H,則PH⊥平面ABCD,求解直角三角形PDH得PH![]() ,再由棱錐體積公式求三棱錐P﹣ABD的體積.
,再由棱錐體積公式求三棱錐P﹣ABD的體積.
(1)證明:取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,
∵![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,
的中點,![]() ,
,
∴![]() .
.
又![]() 是正三角形,
是正三角形,
∴![]() .
.
∵![]() ,
,![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]()
又![]() 平面
平面![]()
∴![]()
(2)∵![]() ,
,![]() ,
,
∴![]() .
.
又![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
過點![]() 作
作![]() ,交
,交![]() 延長線于點
延長線于點![]() ,則
,則![]() 平面
平面![]() .
.
在直角三角形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.


 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:高中數學 來源: 題型:
【題目】基于移動網絡技術的共享單車被稱為“新四大發明”之一,短時間內就風靡全國,給人們帶來新的出行體驗,某共享單車運營公司的市場研究人員為了了解公司的經營狀況,對公司最近6個月的市場占有率![]() 進行了統計,結果如下表:
進行了統計,結果如下表:
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
(1)請用相關系數說明能否用線性回歸模型擬合![]() 與月份代碼
與月份代碼![]() 之間的關系.如果能,請計算出
之間的關系.如果能,請計算出![]() 關于
關于![]() 的線性回歸方程,如果不能,請說明理由;
的線性回歸方程,如果不能,請說明理由;
(2)根據調研數據,公司決定再采購一批單車擴大市場,從成本1000元/輛的![]() 型車和800元/輛的
型車和800元/輛的![]() 型車中選購一種,兩款單車使用壽命頻數如下表:
型車中選購一種,兩款單車使用壽命頻數如下表:
| 1年 | 2年 | 3年 | 4年 | 總計 |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
經測算,平均每輛單車每年能為公司帶來500元的收入,不考慮除采購成本以外的其它成本,假設每輛單車的使用壽命都是整數年,用頻率估計每輛車使用壽命的概率,以平均每輛單車所產生的利潤的估計值為決策依據,如果你是公司負責人,會選擇哪款車型?
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:相關系數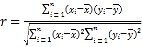 ,
,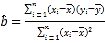 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距等于
的焦距等于![]() ,短軸與長軸的長度比等于
,短軸與長軸的長度比等于![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 在橢圓
在橢圓![]() 上,過
上,過![]() 作兩直線
作兩直線![]() ,分別交橢圓
,分別交橢圓![]() 于另外兩點
于另外兩點![]() ,當
,當![]() 的傾斜角互為補角時,求
的傾斜角互為補角時,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調查機構對某校學生做了一個是否同意生“二孩”抽樣調查,該調查機構從該校隨機抽查了100名不同性別的學生,調查統計他們是同意父母生“二孩”還是反對父母生“二孩”,現已得知100人中同意父母生“二孩”占60%,統計情況如下表:
同意 | 不同意 | 合計 | |
男生 | a | 5 | |
女生 | 40 | d | |
合計 | 100 |
(1)求 a,d 的值;
(2)根據以上數據,能否有97.5%的把握認為是否同意父母生“二孩”與性別有關?請說明理由;
附: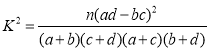
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩名大學生因為學習需要,欲各自選購一臺筆記本電腦,他們決定在A,B,C三個品牌的五款產品中選擇,這五款筆記本電腦在某電商平臺的價格與銷量數據如表所示:
品牌 | A | B | C | ||
型號 | A﹣1 | A﹣2 | B﹣1 | B﹣2 | C﹣1 |
價格(元) | 6000 | 7500 | 10000 | 8000 | 4500 |
銷量(臺) | 1000 | 1000 | 200 | 800 | 3000 |
(Ⅰ)若甲選擇某品牌的筆記本電腦的概率與該品牌的總銷量成正比,求他選擇B品牌的筆記本電腦的概率;
(Ⅱ)若甲、乙兩人選擇每種型號的筆記本電腦的概率都相等,且兩人選購的型號不相同,求他們兩人購買的筆記本電腦的價格之和大于15000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:①若線性回歸方程為![]() ,則當變量
,則當變量![]() 增加一個單位時,
增加一個單位時,![]() 一定增加3個單位;②將一組數據中的每個數據都加上同一個常數后,方差不會改變;③線性回歸直線方程
一定增加3個單位;②將一組數據中的每個數據都加上同一個常數后,方差不會改變;③線性回歸直線方程![]() 必過點
必過點![]() ;④抽簽法屬于簡單隨機抽樣;其中錯誤的說法是( )
;④抽簽法屬于簡單隨機抽樣;其中錯誤的說法是( )
A.①③B.②③④C.①D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() 交于點
交于點![]() ,
,![]() 是
是![]() 上任意一點.
上任意一點.
(1)求證![]() ;
;
(2)已知二面角![]() 的余弦值為
的余弦值為![]() ,若
,若![]() 為
為![]() 的中點,求
的中點,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com