
【題目】在四棱錐![]() 中,側面
中,側面![]() 底面ABCD,底面ABCD為直角梯形,
底面ABCD,底面ABCD為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,E,F分別為AD,PC的中點.
,E,F分別為AD,PC的中點.
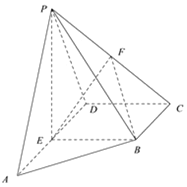
![]() Ⅰ
Ⅰ![]() 求證:
求證:![]() 平面BEF;
平面BEF;
![]() Ⅱ
Ⅱ![]() 若
若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2) ![]() .
.
【解析】
(1)連接![]() 交
交![]() 于
于![]() ,并連接
,并連接![]() ,
,![]() ,由空間幾何關系可證得
,由空間幾何關系可證得![]() ,利用線面平行的判斷定理可得
,利用線面平行的判斷定理可得![]() 平面
平面![]() .
.
(2)(法一)取![]() 中點
中點![]() ,連
,連![]() ,
,![]() ,
,![]() ,由二面角的定義結合幾何體的特征可知
,由二面角的定義結合幾何體的特征可知![]() 為二面角
為二面角![]() 的平面角,計算可得二面角
的平面角,計算可得二面角![]() 的余弦值為
的余弦值為![]() .
.
(法二)以![]() 為原點,
為原點,![]() 、
、![]() 、
、![]() 分別為
分別為![]() 、
、![]() 、
、![]() 建立直角坐標系,則平面
建立直角坐標系,則平面![]() 法向量可取:
法向量可取:![]() ,平面
,平面![]() 的法向量
的法向量![]() ,由空間向量的結論計算可得二面角
,由空間向量的結論計算可得二面角![]() 的余弦值為
的余弦值為![]() .
.
(1)連接![]() 交
交![]() 于
于![]() ,并連接
,并連接![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 為
為![]() 中點,
中點, ![]() ,且
,且![]() ,
,
![]() 四邊形
四邊形![]() 為平行四邊形,
為平行四邊形,![]()
![]() 為
為![]() 中點,又
中點,又![]() 為
為![]() 中點,
中點,
![]()
![]() ,
, ![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(2)(法一)由![]() 為正方形可得
為正方形可得![]() ,
,![]()
![]() .
.
取![]() 中點
中點![]() ,連
,連![]() ,
,![]() ,
,![]() ,
,![]() 側面
側面![]()
![]() 底面
底面![]() ,且交于
,且交于![]() ,
,![]()
![]()
![]() ,
,
![]() 面
面![]() ,又
,又![]() ,
,![]() 為二面角
為二面角![]() 的平面角,
的平面角,
又![]() ,
,![]() ,
,![]() ,
,
![]() ,所以二面角
,所以二面角![]() 的余弦值為
的余弦值為![]() .
.
(法二)由題意可知![]()
![]() 面
面![]() ,
,![]()
![]()
![]() ,如圖所示,以
,如圖所示,以![]() 為原點,
為原點,![]() 、
、![]() 、
、![]() 分別為
分別為![]() 、
、![]() 、
、![]() 建立直角坐標系,則
建立直角坐標系,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
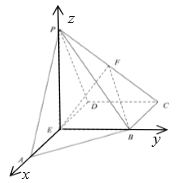
平面![]() 法向量可取:
法向量可取:![]() ,
,
平面![]() 中,設法向量為
中,設法向量為![]() ,則
,則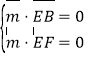
![]()
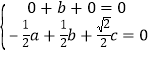 ,
,
取![]() ,
,
![]() ,所以二面角
,所以二面角![]() 的余弦值為
的余弦值為![]() .
.


 課堂練加測系列答案
課堂練加測系列答案 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案科目:高中數學 來源: 題型:
【題目】近年空氣質量逐步惡化,霧霾天氣現象出現增多,大氣污染危害加重.大氣污染可引起心悸、呼吸困難等心肺疾病.為了解某市心肺疾病是否與性別有關,在某醫院隨機對心肺疾病入院的50人進行問卷調查,得到了如下的列聯表:

(1)用分層抽樣的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?
(2)在上述抽取的6人中選2人,求恰好有1名女性的概率;
(3)為了研究心肺疾病是否與性別有關,請計算出統計量![]() ,你有多大把握認為心肺疾病與性別有關?
,你有多大把握認為心肺疾病與性別有關?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的方程為
的方程為![]() ,雙曲線
,雙曲線![]() 的一條漸近線與
的一條漸近線與![]() 軸所成的夾角為
軸所成的夾角為![]() ,且雙曲線的焦距為
,且雙曲線的焦距為![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 分別為橢圓
分別為橢圓![]() 的左,右焦點,過
的左,右焦點,過![]() 作直線
作直線![]() (與
(與![]() 軸不重合)交橢圓于
軸不重合)交橢圓于![]() ,
, ![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,記直線
,記直線![]() 的斜率為
的斜率為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】實數a,b滿足ab>0且a≠b,由a、b、![]() 、
、![]() 按一定順序構成的數列( )
按一定順序構成的數列( )
A. 可能是等差數列,也可能是等比數列
B. 可能是等差數列,但不可能是等比數列
C. 不可能是等差數列,但可能是等比數列
D. 不可能是等差數列,也不可能是等比數列
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,且橢圓
,且橢圓![]() 過點
過點 .過點
.過點![]() 做兩條相互垂直的直線
做兩條相互垂直的直線![]() 、
、![]() 分別與橢圓
分別與橢圓![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四點.
四點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若![]() ,
, ![]() ,探究:直線
,探究:直線![]() 是否過定點?若是,請求出定點坐標;若不是,請說明理由.
是否過定點?若是,請求出定點坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 過點
過點![]() ,且焦點為F,直線l與拋物線相交于A,B兩點.
,且焦點為F,直線l與拋物線相交于A,B兩點.
⑴求拋物線C的方程,并求其準線方程;
⑵![]() 為坐標原點.若
為坐標原點.若![]() ,證明直線l必過一定點,并求出該定點.
,證明直線l必過一定點,并求出該定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C過點M(0,-2)、N(3,1),且圓心C在直線x+2y+1=0上.
(1)求圓C的方程;
(2)設直線ax-y+1=0與圓C交于A,B兩點,是否存在實數a,使得過點P(2,0)的直線l垂直平分弦AB?若存在,求出實數a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,邊a、b、c分別是角A、B、C的對邊,且滿足bcosC=(3a-c)cosB
(1)求cosB
(2)若△ABC的面積為4![]() ,b=4
,b=4![]() ,求△ABC的周長
,求△ABC的周長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,△ABC為正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中點.求證:

(1)DE=DA;
(2)平面BDM⊥平面ECA;
(3)平面DEA⊥平面ECA.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com