
【題目】(本小題滿分12分)求下列函數(shù)的解析式:
(1)已知![]() ,求
,求![]() ;
;
(2) 已知函數(shù)![]() 是一次函數(shù),且滿足關(guān)系式
是一次函數(shù),且滿足關(guān)系式![]() ,求
,求![]() .
.
【答案】(1) f(x)= ![]() (2) f(x)=2x+7
(2) f(x)=2x+7
【解析】試題分析:(1)由![]() ,用
,用![]() 換x得到等式3
換x得到等式3![]() +2f(x)=
+2f(x)= ![]() 兩式聯(lián)立消去
兩式聯(lián)立消去![]() ,即可的結(jié)果;(2 )設(shè)f(x)=ax+b(a≠0)由
,即可的結(jié)果;(2 )設(shè)f(x)=ax+b(a≠0)由![]() 得:3[a(x+1)+b]-2[a(x-1)+b]=ax+5a+b=2x+17,根據(jù)對(duì)應(yīng)項(xiàng)系數(shù)相等,列方程組求得求解即可.
得:3[a(x+1)+b]-2[a(x-1)+b]=ax+5a+b=2x+17,根據(jù)對(duì)應(yīng)項(xiàng)系數(shù)相等,列方程組求得求解即可.
試題解析:(1 )由已知可得![]() , 用
, 用![]() 換x得到等式3
換x得到等式3![]() +2f(x)=
+2f(x)= ![]()
聯(lián)立兩方程可求解出f(x)= ![]() .
.
(2 )設(shè)f(x)=ax+b(a≠0)由![]() 得:3[a(x+1)+b]-2[a(x-1)+b]=ax+5a+b=2x+17∴a=2 且5a+b=17 解得a=2,b=7 ∴f(x)=2x+7
得:3[a(x+1)+b]-2[a(x-1)+b]=ax+5a+b=2x+17∴a=2 且5a+b=17 解得a=2,b=7 ∴f(x)=2x+7


 勵(lì)耘書業(yè)暑假銜接寧波出版社系列答案
勵(lì)耘書業(yè)暑假銜接寧波出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)= ![]() ;
;
(1)若f(x)的定義域?yàn)?/span> (-∞,+∞), 求實(shí)數(shù)a的范圍;
(2)若f(x)的值域?yàn)?/span> [0, +∞), 求實(shí)數(shù)a的范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】沭陽(yáng)縣某水果店銷售某種水果,經(jīng)市場(chǎng)調(diào)查,該水果每日的銷售量![]() (單位:千克)與銷售價(jià)格
(單位:千克)與銷售價(jià)格![]() 近似滿足關(guān)系式
近似滿足關(guān)系式![]() ,其中
,其中![]() 為常數(shù),已知銷售價(jià)格定為
為常數(shù),已知銷售價(jià)格定為![]() 元
元![]() 千克時(shí),每日可銷售出該水果
千克時(shí),每日可銷售出該水果![]() 千克.
千克.
(1)求實(shí)數(shù)![]() 的值;
的值;
(2)若該水果的成本價(jià)格為![]() 元
元![]() 千克,要使得該水果店每日銷售該水果獲得最大利潤(rùn),請(qǐng)你確定銷售價(jià)格
千克,要使得該水果店每日銷售該水果獲得最大利潤(rùn),請(qǐng)你確定銷售價(jià)格![]() 的值,并求出最大利潤(rùn).
的值,并求出最大利潤(rùn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() +
+![]() =1(a>b>0)的左焦點(diǎn)為F,右頂點(diǎn)為A,拋物線y2=
=1(a>b>0)的左焦點(diǎn)為F,右頂點(diǎn)為A,拋物線y2=![]() (a+c)x與橢圓交于B,C兩點(diǎn),若四邊形ABFC是菱形,則橢圓的離心率等于( )
(a+c)x與橢圓交于B,C兩點(diǎn),若四邊形ABFC是菱形,則橢圓的離心率等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司試銷一種成本單價(jià)為500元/件的新產(chǎn)品,規(guī)定試銷時(shí)銷售單價(jià)不低于成本單價(jià),又不高于800元/件.經(jīng)試銷調(diào)查,發(fā)現(xiàn)銷售量![]() (件)與銷售單價(jià)
(件)與銷售單價(jià)![]() (元/件)可近似看作一次函數(shù)
(元/件)可近似看作一次函數(shù)![]() 的關(guān)系(如圖所示).
的關(guān)系(如圖所示).
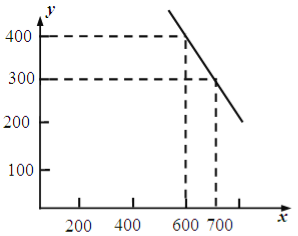
(1)根據(jù)圖象,求一次函數(shù)![]() 的表達(dá)式;
的表達(dá)式;
(2)設(shè)公司獲得的毛利潤(rùn)(毛利潤(rùn)=銷售總價(jià)—成本總價(jià))為![]() 元. 試用銷售單價(jià)
元. 試用銷售單價(jià)![]() 表示毛利潤(rùn)
表示毛利潤(rùn)![]() 并求銷售單價(jià)定為多少時(shí),該公司獲得最大毛利潤(rùn)?最大毛利潤(rùn)是多少?此時(shí)的銷售量是多少?
并求銷售單價(jià)定為多少時(shí),該公司獲得最大毛利潤(rùn)?最大毛利潤(rùn)是多少?此時(shí)的銷售量是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=ln x+![]() +ax(a是實(shí)數(shù)),g(x)=
+ax(a是實(shí)數(shù)),g(x)=![]() +1.
+1.
(1)當(dāng)a=2時(shí),求函數(shù)f(x)在定義域上的最值;
(2)若函數(shù)f(x)在[1,+∞)上是單調(diào)函數(shù),求a的取值范圍;
(3)是否存在正實(shí)數(shù)a滿足:對(duì)于任意x1∈[1,2],總存在x2∈[1,2],使得f(x1)=g(x2)成立? 若存在,求出a的取值范圍,若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為參加學(xué)校的“我愛古詩(shī)詞”知識(shí)競(jìng)賽,小王所在班級(jí)組織了一次古詩(shī)詞知識(shí)測(cè)試,并將全班同學(xué)的分?jǐn)?shù)(得分取正整數(shù),滿分為100分)進(jìn)行統(tǒng)計(jì),以下是根據(jù)這次測(cè)試成績(jī)制作的不完整的頻率分布表和頻率分布直方圖.
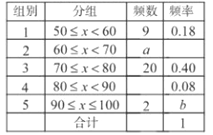

請(qǐng)根據(jù)以上頻率分布表和頻率分布直方圖,回答下列問(wèn)題:
(1)求出![]() 的值;
的值;
(2)老師說(shuō):“小王的測(cè)試成績(jī)是全班同學(xué)成績(jī)的中位數(shù)”,那么小王的測(cè)試成績(jī)?cè)谑裁捶秶鷥?nèi)?
(3)若要從小明、小敏等五位成績(jī)優(yōu)秀的同學(xué)中隨機(jī)選取兩位參加競(jìng)賽,請(qǐng)用:列表法或樹狀圖求出小明、小敏同時(shí)被選中的概率.(注:五位同學(xué)請(qǐng)用![]() 表示,其中小明為
表示,其中小明為![]() ,小敏為
,小敏為![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】甲、乙兩人各進(jìn)行3次射擊,甲每次擊中目標(biāo)的概率為![]() ,乙每次擊中目標(biāo)的概率為
,乙每次擊中目標(biāo)的概率為![]() 求:(1)甲恰好擊中目標(biāo)2次的概率;(2)乙至少擊中目標(biāo)2次的概率;
求:(1)甲恰好擊中目標(biāo)2次的概率;(2)乙至少擊中目標(biāo)2次的概率;
(3)乙恰好比甲多擊中目標(biāo)2次的概率
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知斜三棱柱![]() 的底面是直角三角形,
的底面是直角三角形,![]() ,側(cè)棱與底面所成角為
,側(cè)棱與底面所成角為![]() ,點(diǎn)
,點(diǎn)![]() 在底面上身影
在底面上身影![]() 落在
落在![]() 上.
上.

(1)求證:![]() 平面
平面![]() ;
;
(2)若點(diǎn)![]() 恰為
恰為![]() 中點(diǎn),且
中點(diǎn),且![]() ,求
,求![]() 的大小;
的大小;
(3)若![]() ,且當(dāng)
,且當(dāng)![]() 時(shí),求二面角
時(shí),求二面角![]() 的大小.
的大小.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com