
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)討論函數(shù)![]() 的零點(diǎn)個(gè)數(shù);
的零點(diǎn)個(gè)數(shù);
(2)求證:![]() .
.
【答案】(1)見解析(2)見解析
【解析】試題分析:(1)對(duì)函數(shù)求導(dǎo),研究函數(shù)的單調(diào)性,進(jìn)而得到函數(shù)的變化趨勢(shì),結(jié)合圖像得到函數(shù)的零點(diǎn)個(gè)數(shù);(2)不等式![]() 可化為
可化為![]() ,記
,記![]() ,證得
,證得![]() 即可.
即可.
詳解:(1)由題,![]() ,所以當(dāng)
,所以當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)遞增,當(dāng)
上單調(diào)遞增,當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)遞減,∴
上單調(diào)遞減,∴![]() 有極大值
有極大值![]() .
.
且當(dāng)![]() 時(shí),
時(shí),![]() ;
;![]() 時(shí),
時(shí),![]() ,所以,當(dāng)
,所以,當(dāng)![]() 或
或![]() 時(shí),
時(shí),![]() 恰有一個(gè)零點(diǎn);
恰有一個(gè)零點(diǎn);![]() 時(shí),
時(shí),![]() 有兩個(gè)零點(diǎn);
有兩個(gè)零點(diǎn);![]() 時(shí),
時(shí),![]() 沒有零點(diǎn).
沒有零點(diǎn).
(2)由(1)可知,![]() .①當(dāng)
.①當(dāng)![]() 時(shí),不等式
時(shí),不等式![]() 可化為
可化為![]() ,記
,記![]() ,得
,得![]() .
.
設(shè)![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞增,又
上單調(diào)遞增,又![]() ,
,![]() ,
,![]() 在
在![]() 上圖象是不間斷的,
上圖象是不間斷的,
∴存在唯一的實(shí)數(shù)![]() ,使得
,使得![]() ,∴當(dāng)
,∴當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,
,![]() 在
在![]() 上遞減,當(dāng)
上遞減,當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,
,![]() 在
在![]() 上遞增,
上遞增,
∴當(dāng)![]() 時(shí),
時(shí),![]() 有極小值,即為最小值,
有極小值,即為最小值,![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
所以,![]() ,即
,即![]() .
.
②當(dāng)![]() 時(shí),設(shè)
時(shí),設(shè)![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞減,∴
上單調(diào)遞減,∴![]() ,
,
所以![]() ,
,
綜上所述,![]() .
.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(2018·江西六校聯(lián)考)在△ABC中,角A,B,C所對(duì)的邊分別為a,b,c,a=4![]() ,b=4,cosA=-
,b=4,cosA=-![]() .
.
(1)求角B的大小;
(2)若f(x)=cos2x+![]() sin2(x+B),求函數(shù)f(x)的單調(diào)遞增區(qū)間.
sin2(x+B),求函數(shù)f(x)的單調(diào)遞增區(qū)間.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在著名的漢諾塔問題中,有三根高度相同的柱子和一些大小及顏色各不相同的圓盤,三根柱子分別為起始柱、輔助柱及目標(biāo)柱.已知起始柱上套有![]() 個(gè)圓盤,較大的圓盤都在較小的圓盤下面.現(xiàn)把圓盤從起始柱全部移到目標(biāo)柱上,規(guī)則如下:每次只能移動(dòng)一個(gè)圓盤,且每次移動(dòng)后,每根柱上較大的圓盤不能放在較小的圓盤上面,規(guī)定一個(gè)圓盤從任一根柱上移動(dòng)到另一根柱上為一次移動(dòng).若將
個(gè)圓盤,較大的圓盤都在較小的圓盤下面.現(xiàn)把圓盤從起始柱全部移到目標(biāo)柱上,規(guī)則如下:每次只能移動(dòng)一個(gè)圓盤,且每次移動(dòng)后,每根柱上較大的圓盤不能放在較小的圓盤上面,規(guī)定一個(gè)圓盤從任一根柱上移動(dòng)到另一根柱上為一次移動(dòng).若將![]() 個(gè)圓盤從起始柱移動(dòng)到目標(biāo)柱上最少需要移動(dòng)的次數(shù)記為
個(gè)圓盤從起始柱移動(dòng)到目標(biāo)柱上最少需要移動(dòng)的次數(shù)記為![]() ,則
,則![]() ( )
( )

A. 33B. 31C. 17D. 15
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市地鐵全線共有四個(gè)車站,甲、乙兩人同時(shí)在地鐵第1號(hào)車站(首發(fā)站)乘車,假設(shè)每人自第2號(hào)站開始,在每個(gè)車站下車是等可能的,約定用有序?qū)崝?shù)對(duì)![]() 表示“甲在
表示“甲在![]() 號(hào)車站下車,乙在
號(hào)車站下車,乙在![]() 號(hào)車站下車”
號(hào)車站下車”
(Ⅰ)用有序?qū)崝?shù)對(duì)把甲、乙兩人下車的所有可能的結(jié)果列舉出來;
(Ⅱ)求甲、乙兩人同在第3號(hào)車站下車的概率;
(Ⅲ)求甲、乙兩人在不同的車站下車的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校從參加某次知識(shí)競(jìng)賽的1000同學(xué)中,隨機(jī)抽取60名同學(xué)將其成績(jī)(百分制,均為整數(shù))分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六組后,得到部分頻率分布直方圖(如圖),觀察圖形中的信息,回答下列問題:
六組后,得到部分頻率分布直方圖(如圖),觀察圖形中的信息,回答下列問題:
(1)補(bǔ)全頻率分布直方圖,并估計(jì)本次知識(shí)競(jìng)賽的均分;

(2)如果確定不低于85分的同學(xué)進(jìn)入復(fù)賽,問這1000名參賽同學(xué)中估計(jì)有多少人進(jìn)人復(fù)賽;
(3)若從第一組,第二組和第六組三組學(xué)生中分層抽取6人,再?gòu)倪@6人中隨機(jī)抽取2人,求所抽取的2人成績(jī)之差的絕對(duì)值大于20的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義一:對(duì)于一個(gè)函數(shù)![]() ,若存在兩條距離為
,若存在兩條距離為![]() 的直線
的直線![]() 和
和![]() ,使得
,使得![]() 時(shí),
時(shí),![]() 恒成立,則稱函數(shù)
恒成立,則稱函數(shù)![]() 在
在![]() 內(nèi)有一個(gè)寬度為
內(nèi)有一個(gè)寬度為![]() 的通道.
的通道.
定義二:若一個(gè)函數(shù)![]() 對(duì)于任意給定的正數(shù)
對(duì)于任意給定的正數(shù)![]() ,都存在一個(gè)實(shí)數(shù)
,都存在一個(gè)實(shí)數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 在
在![]() 內(nèi)有一個(gè)寬度為
內(nèi)有一個(gè)寬度為![]() 的通道,則稱
的通道,則稱![]() 在正無窮處有永恒通道.
在正無窮處有永恒通道.
下列函數(shù)①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() . 其中在正無窮處有永恒通道的函數(shù)序號(hào)是 .
. 其中在正無窮處有永恒通道的函數(shù)序號(hào)是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(13分)設(shè){an}是公比為正數(shù)的等比數(shù)列a1=2,a3=a2+4.
(Ⅰ)求{an}的通項(xiàng)公式;
(Ⅱ)設(shè){bn}是首項(xiàng)為1,公差為2的等差數(shù)列,求數(shù)列{an+bn}的前n項(xiàng)和Sn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某生物小組為了研究溫度對(duì)某種酶的活性的影響進(jìn)行了一組實(shí)驗(yàn),得到的實(shí)驗(yàn)數(shù)據(jù)經(jīng)整理得到如下的折線圖:
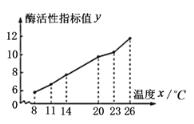
(1)由圖可以看出,這種酶的活性![]() 與溫度
與溫度![]() 具有較強(qiáng)的線性相關(guān)性,請(qǐng)用相關(guān)系數(shù)加以說明;
具有較強(qiáng)的線性相關(guān)性,請(qǐng)用相關(guān)系數(shù)加以說明;
(2)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程,并預(yù)測(cè)當(dāng)溫度為
的線性回歸方程,并預(yù)測(cè)當(dāng)溫度為![]() 時(shí),這種酶的活性指標(biāo)值.(計(jì)算結(jié)果精確到0.01)
時(shí),這種酶的活性指標(biāo)值.(計(jì)算結(jié)果精確到0.01)
參考數(shù)據(jù):![]() ,
,![]() ,
,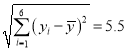 ,
,![]() .
.
參考公式:相關(guān)系數(shù)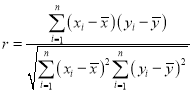 .
.
回歸直線方程![]() ,
,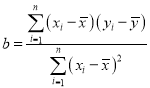 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)F是拋物線C:y2=2px(p>0)的焦點(diǎn),點(diǎn)M(x0,1)在C上,且|MF|=![]() .
.
(1)求p的值;
(2)若直線l經(jīng)過點(diǎn)Q(3,-1)且與C交于A,B(異于M)兩點(diǎn),證明:直線AM與直線BM的斜率之積為常數(shù).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com