
【題目】(2018·江西六校聯考)在△ABC中,角A,B,C所對的邊分別為a,b,c,a=4![]() ,b=4,cosA=-
,b=4,cosA=-![]() .
.
(1)求角B的大小;
(2)若f(x)=cos2x+![]() sin2(x+B),求函數f(x)的單調遞增區間.
sin2(x+B),求函數f(x)的單調遞增區間.
【答案】(1)![]() (2)
(2)![]()
【解析】
試題分析:(1)根據平方關系求sinA,再根據正弦定理求sinB,即得角B的大小;(2)先根據兩角和正弦公式以及配角公式將函數化為基本三角函數形式,再根據正弦函數性質求單調區間.
試題解析:(1)在△ABC中,由cosA=-![]() ,得sinA=
,得sinA=![]() .
.
由![]() =
=![]() ,得sinB=
,得sinB=![]() .又由b<a,得B<A,所以B=
.又由b<a,得B<A,所以B=![]() .
.
(2)由余弦定理a2=b2+c2-2bccosA,得48=16+c2+4c,
解得c=4,c=-8(舍去).
所以f(x)=cos2x+2sin2![]() =cos2x+1-cos2
=cos2x+1-cos2![]() =cos2x+1-
=cos2x+1-![]() cos2x+
cos2x+![]() sin2x=1+sin
sin2x=1+sin![]()
由-![]() +2kπ≤2x+
+2kπ≤2x+![]() ≤
≤![]() +2kπ(k∈Z),得
+2kπ(k∈Z),得
-![]() +kπ≤x≤
+kπ≤x≤![]() +kπ(k∈Z).
+kπ(k∈Z).
所以函數f(x)的單調遞增區間為![]() ,k∈Z.
,k∈Z.


科目:高中數學 來源: 題型:
【題目】某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:![]() )有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間
)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間![]() ,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
![]()
以最高氣溫位于各區間的頻率估計最高氣溫位于該區間的概率.
(1)求六月份這種酸奶一天的需求量![]() (單位:瓶)的分布列;
(單位:瓶)的分布列;
(2)設六月份一天銷售這種酸奶的利潤為![]() (單位:元),當六月份這種酸奶一天的進貨量
(單位:元),當六月份這種酸奶一天的進貨量![]() (單位:瓶)為多少時,
(單位:瓶)為多少時,![]() 的數學期望達到最大值?
的數學期望達到最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
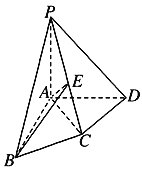
【題目】如圖,在四棱錐![]() 中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點.證明:
中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點.證明:
(1)CD⊥AE;
(2)PD⊥平面ABE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題:
①若樣本數據![]() 的方差為
的方差為![]() ,則數據
,則數據![]() 的方差為
的方差為![]() ;
;
②“平面向量![]() 的夾角為銳角,則
的夾角為銳角,則![]() ”的逆命題為真命題;
”的逆命題為真命題;
③命題“![]() ,均有
,均有![]() ”的否定是“
”的否定是“![]() ,均有
,均有![]() ”;
”;
④![]() 是直線
是直線![]() 與直線
與直線![]() 平行的必要不充分條件.
平行的必要不充分條件.
其中正確的命題個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com