
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)設![]() ,求函數
,求函數![]() 在區間
在區間![]() 上的最小值;
上的最小值;
(3)某同學發現:總存在正實數![]() ,
,![]() ,使
,使![]() ,試問:該同學的判斷是否正確?若不正確,請說明理由;若正確,請直接寫出
,試問:該同學的判斷是否正確?若不正確,請說明理由;若正確,請直接寫出![]() 的取值范圍(不需要解答過程).
的取值范圍(不需要解答過程).
【答案】(1)單調增區間為![]() ,
, ![]() ;(2)
;(2)![]() 時,
時,![]() ;若
;若![]() 時,
時,![]() .(3)正確,
.(3)正確,![]() 的取值范圍為
的取值范圍為![]() .
.
【解析】
(1)先確定函數定義域,再利用導數,可求函數![]() 的單調區間;
的單調區間;
(2)根據![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,結合函數定義域分類討論可求出函數
上單調遞減,結合函數定義域分類討論可求出函數![]() 在區間
在區間![]() 上的最小值;
上的最小值;
(3)![]() 的取值范圍為
的取值范圍為![]() ,根據
,根據![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,結合函數圖象即可求得.
上單調遞減,結合函數圖象即可求得.
解(1)定義域![]() ,
,![]() ,
,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,所以
,所以![]() 單調增區間為
單調增區間為![]() ;
;
當![]() 時,
時,![]() ,所以
,所以![]() 的單調增區間為
的單調增區間為![]() ;
;
(2)由(1)知![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,所以
上單調遞減,所以
當![]() 時,即
時,即![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() .
.
當![]() 時,即
時,即![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() ,由于
,由于![]() ,
,
若![]() 時,
時,![]() ;
;
若![]() 時,
時,![]() .
.
當![]() 時,即
時,即![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,
,
綜上得:若![]() 時,
時,![]() ;
;
若![]() 時,
時,![]() ;
;
(3)正確,![]() 的取值范圍為
的取值范圍為![]() .
.
注:理由如下,考慮幾何意義,當![]() 時,
時,![]() ,
,
由于![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
所以![]() 的圖象大致如下圖所示,
的圖象大致如下圖所示,
所以總存在正實數![]() ,
,![]() 且
且![]() ,使得
,使得![]() ,即
,即![]() ,即
,即![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】合肥一中、六中為了加強交流,增進友誼,兩校準備舉行一場足球賽,由合肥一中版畫社的同學設計一幅矩形宣傳畫,要求畫面面積為![]() ,畫面的上、下各留
,畫面的上、下各留![]() 空白,左、右各留
空白,左、右各留![]() 空白.
空白.

(1)如何設計畫面的高與寬的尺寸,才能使宣傳畫所用紙張面積最小?
(2)設畫面的高與寬的比為![]() ,且
,且![]() ,求
,求![]() 為何值時,宣傳畫所用紙張面積最小?
為何值時,宣傳畫所用紙張面積最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是圓O的直徑,C是圓上的點,平面PAC⊥平面ABC,PA⊥AB.
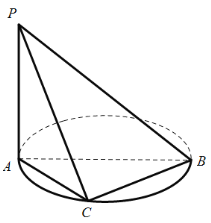
(1)求證:PA⊥平面ABC;
(2)若PA=AC=2,求點A到平面PBC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“珠算之父”程大位是我國明代著名的數學家,他的應用巨著《算法統綜》中有一首“竹筒容米”問題:“家有九節竹一莖,為因盛米不均平,下頭三節四升五,上梢四節三升八,唯有中間兩節竹,要將米數次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容積依次相差同一數量.)用你所學的數學知識求得中間兩節竹的容積為
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常數).
為常數).
(Ⅰ)討論函數![]() 的單調性;
的單調性;
(Ⅱ)是否存在正實數![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,若存在,求出實數
,若存在,求出實數![]() 的取值范圍;若不存在,請說明理由;
的取值范圍;若不存在,請說明理由;
(Ⅲ)當![]() 時,
時, ![]() ,對
,對![]() 恒成立,求整數
恒成立,求整數![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:在平面四邊形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() (如圖1),若將
(如圖1),若將![]() 沿對角線BD折疊,使
沿對角線BD折疊,使![]() (如圖2).請在圖2中解答下列問題.
(如圖2).請在圖2中解答下列問題.
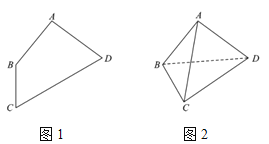
(1)證明:![]() ;
;
(2)求三棱錐![]() 的高.
的高.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),圓
為參數),圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的方程和圓
的方程和圓![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 為圓
為圓![]() 上一動點,求點
上一動點,求點![]() 到直線
到直線![]() 的最小距離.
的最小距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com