
���}Ŀ����֪�E�A![]() ��
��![]() ��������c(di��n)�քe��C��D�����^�c(di��n)
��������c(di��n)�քe��C��D�����^�c(di��n)![]() ��P�ǙE�A�Ϯ���C��D������һ�c(di��n)��ֱ��PC��PD��б��֮�e��
��P�ǙE�A�Ϯ���C��D������һ�c(di��n)��ֱ��PC��PD��б��֮�e��![]() ��
��
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2��O������(bi��o)ԭ�c(di��n)���O(sh��)ֱ��CP����ֱ��x = m���c(di��n)M����(d��ng)m���ֵ�r(sh��)��![]() �鶨ֵ��
�鶨ֵ��
���𰸡���1��![]() ��2��
��2��![]()
��������
(1)�O(sh��)![]() ,����(j��)�}������
,����(j��)�}������![]() ,�ٴ�
,�ٴ�![]() ��E�A���̼������.
��E�A���̼������.
(2)����(j��)(1)�еĽY(ji��)Փ, �O(sh��)ֱ��![]() ,��(li��n)���c�E�A�ķ���,���
,��(li��n)���c�E�A�ķ���,���![]() ,
,![]() ,�ٱ��_(d��)��
,�ٱ��_(d��)��![]() ,����(j��)��������}���ϵ��(sh��)���P(gu��n)ϵ����.Ҳ��ֱ���O(sh��)
,����(j��)��������}���ϵ��(sh��)���P(gu��n)ϵ����.Ҳ��ֱ���O(sh��)![]() ���_(d��)��
���_(d��)��![]() ,����
,����![]() �M��E�A�ķ����M(j��n)�л���,ͬ���ɵ�m��ֵ.
�M��E�A�ķ����M(j��n)�л���,ͬ���ɵ�m��ֵ.
�⣺��1���E�A![]() �^�c(di��n)
�^�c(di��n)![]() ,��
,��![]() ,��
,��
����?y��n)�ֱ��![]() ��б��֮�e��
��б��֮�e��![]() ,��
,��![]() .
.
��![]() .��
.��![]() ,��
,��
(li��n)���٢ڵ�![]() ��
��
������ęE�A���̞�![]() ��
��
��2������1���ɣ�1��֪,![]() �����}����O(sh��)
�����}����O(sh��)![]() ,
,
��x=m,��![]() �����O(sh��)
�����O(sh��)![]()
�� �����ã�
�����ã�![]() ��
��
��![]() ,��
,��![]() ,
,![]() ,
,
����![]() ,
,
��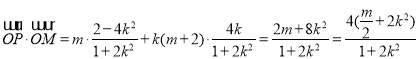 ,
,
Ҫʹ![]() �ck�o�P(gu��n),ֻ��
�ck�o�P(gu��n),ֻ��![]() ,�˕r(sh��)
,�˕r(sh��)![]() �����4.
�����4.
��![]()
����2��:�O(sh��)![]() ,�t
,�t![]() ,��x=m,��
,��x=m,��![]() ,
,
��![]()
��![]() ��
��![]() ,
,
����![]() ,
,
Ҫʹ![]() �c
�c![]() �o�P(gu��n),ֻ�
�o�P(gu��n),ֻ�![]() ,�˕r(sh��)
,�˕r(sh��)![]() .
.
��![]()


 Ӣ��Ӌ(j��)��ͬ���n�r(sh��)��ЧӖ(x��n)��ϵ�д�
Ӣ��Ӌ(j��)��ͬ���n�r(sh��)��ЧӖ(x��n)��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() �ĘOֵ��
�ĘOֵ��
��2����(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() �ĈD���c����(sh��)
�ĈD���c����(sh��)![]() �ĈD����Ψһ�Ľ��c(di��n)����
�ĈD����Ψһ�Ľ��c(di��n)����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ����
����![]()
��1����(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2�����P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() �������������(sh��)
�������������(sh��)![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������(sh��)y=f��x����x��[1��+�ޣ�����(sh��)��{an}�M��![]() ��
��
�ٺ���(sh��)f��x����������(sh��)��
�ڔ�(sh��)��{an}���f����(sh��)�У�
����һ��(g��)�M��ٵĺ���(sh��)f��x���Ľ���ʽ______��
����һ��(g��)�M��ڵ����M��ٵĺ���(sh��)f��x���Ľ���ʽ______��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����(sh��)��![]() ��
�� ![]() �M�㣺
�M�㣺 ![]() ��ӛ
��ӛ![]() ��ǰ
��ǰ![]() �(xi��ng)�͞�
�(xi��ng)�͞�![]() ����Ҏ(gu��)��
����Ҏ(gu��)��![]() �����x����
�����x����![]() ��
�� ![]()
![]() ��
�� ![]() ��
��
������(sh��)��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��
��
����������![]() ��
�� ![]() ���C����
���C���� ![]() ��
��
���o��������(sh��)![]() �������НM��
�������НM��![]() �Ĕ�(sh��)��
�Ĕ�(sh��)��![]() ����
����![]() ��Ԫ��(g��)��(sh��)����Сֵ��
��Ԫ��(g��)��(sh��)����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() �ăɂ�(g��)���c(di��n)֮��Ľ^��ֵ����Сֵ��
�ăɂ�(g��)���c(di��n)֮��Ľ^��ֵ����Сֵ��![]() ��������(sh��)
��������(sh��)![]() �ĈD������ƽ��
�ĈD������ƽ��![]() ��(g��)��λ�L�ȵõ�����(sh��)
��(g��)��λ�L�ȵõ�����(sh��)![]() �ĈD�t�����f�����_���ǣ� ��
�ĈD�t�����f�����_���ǣ� ��
�ٺ���(sh��)![]() ����С�����ڞ�
����С�����ڞ�![]() ���ں���(sh��)
���ں���(sh��)![]() �ĈD���P(gu��n)���c(di��n)(
�ĈD���P(gu��n)���c(di��n)(![]() )���Q��
)���Q��
�ۺ���(sh��)![]() �ĈD���P(gu��n)��ֱ��
�ĈD���P(gu��n)��ֱ��![]() ���Q���ܺ���(sh��)
���Q���ܺ���(sh��)![]() ��
��![]() �φ��{(di��o)�f��.
�φ��{(di��o)�f��.
A.�٢ڢۢ�B.�٢�C.�ڢۢ�D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������ij̴�λ�ڡ��㷨�y(t��ng)�ڡ��У�1592�꣩�����@ô��(g��)�㷨���E������ͬ����ʮϡ�����÷��إһ֦�����ӈF(tu��n)�A�����£�����������֪.������˼���f����ij��(g��)��(sh��)��������(sh��)������С������(sh��)ֵ�����Ԍ�ij��(sh��)����3���õ�����(sh��)����70������5���õ�����(sh��)����21������7���õ�����(sh��)����15���ٌ����õ�����(g��)�e��ӣ�����Μpȥ105���p����С��105��ֹ�����ýY(ji��)�������@��(g��)��(sh��)����С������(sh��)ֵ.���O���㽛(j��ng)������һ���O�����������ﲻ֪��(sh��)�����}���������ﲻ֪�䔵(sh��)��������(sh��)֮��������唵(sh��)֮���������ߔ�(sh��)֮����������.����������㷨���E���㣬ԓ��Ʒ�����ǎ��� ��
A.21B.22C.23D.24
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���タC��![]() �Ľ��c(di��n)��F��Q�ǒ��タ�ϵ�һ�c(di��n)��
�Ľ��c(di��n)��F��Q�ǒ��タ�ϵ�һ�c(di��n)��![]() ��
��
�������タC�ķ��̣�
�����^�c(di��n)![]() ��ֱ��l�c���タC����M��N���c(di��n)����x�S���Ƿ����һ�c(di��n)A��ʹ��x�Sƽ��
��ֱ��l�c���タC����M��N���c(di��n)����x�S���Ƿ����һ�c(di��n)A��ʹ��x�Sƽ��![]() �������ڣ�����c(di��n)A������(bi��o)���������ڣ�Ո�f�����ɣ�
�������ڣ�����c(di��n)A������(bi��o)���������ڣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() .
.
��1����(d��ng)![]() �r(sh��)��������
�r(sh��)��������![]() �c
�c![]() �Ĺ��о����̣�
�Ĺ��о����̣�
��2����![]() �Ѓɂ�(g��)�Oֵ�c(di��n)
�Ѓɂ�(g��)�Oֵ�c(di��n)![]() ��
��![]() ����
����![]() ����(sh��)��(sh��)a��ȡֵ����.
����(sh��)��(sh��)a��ȡֵ����.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com