【題目】已知橢圓
的離心率為
，過右焦點
作兩條互相垂直的直線
，分別交橢圓
于
和
四點.設
的中點為
.
(1)求橢圓的方程；
(2)直線
是否經過定點？若是，求出定點坐標；若否，請說明理由.
【答案】（1）
；（2）直線
經過定點，定點坐標為
，理由見解析.
【解析】
（1）根據題意確定出c與e的值，利用離心率公式求出a的值，進而求出b的值，代入橢圓方程得答案；
（2）由直線AB與CD斜率存在，設為k，表示出AB方程，設出A與B坐標，進而表示出M的坐標，聯立直線AB與橢圓方程，消去y得關于x的一元二次方程，利用韋達定理表示出M，同理表示N，根據M,N的橫坐標相同求出k的值，得到此時MN斜率不存在，直線恒過定點；若直線MN斜率存在，表示MN的斜率，進而表示直線MN的方程，令
，求出x的值，得到直線MN恒過定點；顯然直線AB或CD斜率不存在，也成立，綜上，得到直線MN恒過定點，求出坐標即可.
（1）因為橢圓的右焦點
，所以
，
又離心率
，所以
，即
故橢圓
的方程為
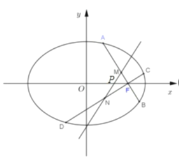
（2）當直線AB和CD斜率存在時
設直線AB方程為：
，再設
則有中點
聯立方程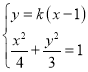
，消去y得：
由韋達定理得： 
，所以M的坐標為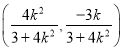
將上式中的k換成
，同理可得N的坐標為
若
，即
，
，
此時直線MN斜率不存在，直線過定點 ；
當
時，即直線MN斜率存在，則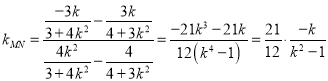
直線MN為
令，得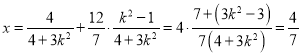
此時直線MN過定點
顯然當直線AB或CD斜率不存在時，直線MN就是x軸，也會過
綜上所述：直線經過定點，定點坐標為
科目：高中數學 來源： 題型：
【題目】拋物線
的焦點為F，圓
，點
為拋物線上一動點.已知當
的面積為
.
（I）求拋物線方程；
（II）若
，過P做圓C的兩條切線分別交y軸于M，N兩點，求
面積的最小值，并求出此時P點坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】足球是世界普及率最高的運動，我國大力發展校園足球.為了解本地區足球特色學校的發展狀況，社會調查小組得到如下統計數據：
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色學校y（百個） | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
（1）根據上表數據，計算y與x的相關系數r，并說明y與x的線性相關性強弱.
（已知：
，則認為y與x線性相關性很強；
，則認為y與x線性相關性一般；
，則認為y與x線性相關性較）：
（2）求y關于x的線性回歸方程，并預測A地區2020年足球特色學校的個數（精確到個）.
參考公式和數據：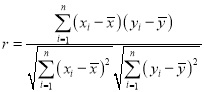
，
，
.
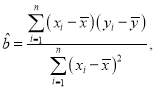
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
的離心率
，左、右焦點分別為
，拋物線
的焦點F恰好是該橢圓的一個頂點．
(1)求橢圓C的方程；
(2)已知圓M：
的切線
與橢圓相交于A、B兩點，那么以AB為直徑的圓是否經過定點？如果是，求出定點的坐標；如果不是，請說明理由，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個盒子中裝有大量形狀大小一樣但重量不盡相同的小球，從中隨機抽取
個作為樣本，稱出它們的重量(單位:克)重量分組區間為
，
，
，
，由此得到樣本的重量頻率分布直方圖（如圖）.
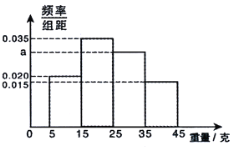
（1）求
的值，并根據樣本數據，估計盒子中小球重量的眾數與平均數（精確到0.01）；
（2）從盒子中裝的大量小球中，隨機抽取3個小球，其中重量在內的小球個數為
，求的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
