
【題目】在四棱錐![]() 中,
中,![]() ,
,![]() .
.

(Ⅰ)若點![]() 為
為![]() 的中點,求證:
的中點,求證:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)當平面![]() 平面
平面![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析; (2)![]() .
.
【解析】
(I)結合平面與平面平行判定,得到平面BEM平行平面PAD,結合平面與平面性質,證明結論.(II)建立空間坐標系,分別計算平面PCD和平面PDB的法向量,結合向量數量積公式,計算余弦值,即可.
(Ⅰ)取![]() 的中點為
的中點為![]() ,連結
,連結![]() ,
,![]() .
.
由已知得,![]() 為等邊三角形,
為等邊三角形,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() .
.
∵![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點,∴
的中點,∴![]() ∥
∥![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() .
.
∵![]() ,∴平面
,∴平面![]() ∥平面
∥平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() .
.
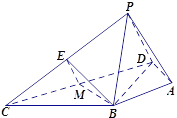
(Ⅱ)連結![]() ,交
,交![]() 于點
于點![]() ,連結
,連結![]() ,由對稱性知,
,由對稱性知,![]() 為
為![]() 的中點,且
的中點,且![]() ,
,![]() .
.
∵平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
以![]() 為坐標原點,
為坐標原點,![]() 的方向為
的方向為![]() 軸正方向,建立空間直角坐標系
軸正方向,建立空間直角坐標系![]() .
.
則![]() (0,
(0,![]() ,0),
,0),![]() (3,0,0),
(3,0,0),![]() (0,0,1).
(0,0,1).
易知平面![]() 的一個法向量為
的一個法向量為![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
則![]() ,
,![]() ,∴
,∴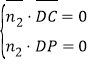 ,
,
∵![]() ,
,![]() ,∴
,∴![]() .
.
令![]() ,得
,得![]() ,∴
,∴![]() ,
,
∴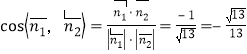 .
.
設二面角![]() 的大小為
的大小為![]() ,則
,則![]() .
.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:高中數學 來源: 題型:
【題目】近幾年出現各種食品問題,食品添加劑會引起血脂增高、血壓增高、血糖增高等疾病.為了解三高疾病是否與性別有關,醫院隨機對入院的60人進行了問卷調查,得到了如下的列聯表:
患三高疾病 | 不患三高疾病 | 合計 | |
男 | 6 | 30 | |
女 | |||
合計 | 36 |
(1)請將如圖的列聯表補充完整;若用分層抽樣的方法在患三高疾病的人群中抽![]() 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)為了研究三高疾病是否與性別有關,請計算出統計量![]() ,并說明你有多大的把握認為三高疾病與性別有關?
,并說明你有多大的把握認為三高疾病與性別有關?
下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校或班級舉行活動,通常需要張貼海報進行宣傳.現讓你設計一張如圖所示的豎向張貼的海報,要求版心面積為128 dm2,上、下兩邊各空2 dm,左、右兩邊各空1 dm.如何設計海報的尺寸,才能使四周空白面積最小?
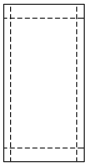
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(1)若函數![]() 在區間
在區間![]() 上是單調函數,試求實數
上是單調函數,試求實數![]() 的取值范圍;
的取值范圍;
(2)已知函數![]() ,且
,且![]() ,若函數
,若函數![]() 在區間
在區間![]() 上恰有3個零點,求實數
上恰有3個零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某位同學進行寒假社會實踐活動,為了對白天平均氣溫與某奶茶店的某種飲料銷量之間的關系進行分析研究,他分別記錄了1月11日至1月15日的白天平均氣溫![]() 與該小賣部的這種飲料銷量
與該小賣部的這種飲料銷量![]() (杯),得到如下數據:
(杯),得到如下數據:
日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均氣溫 | 9 | 10 | 12 | 11 | 8 |
銷量 | 23 | 25 | 30 | 26 | 21 |
(1)若先從這五組數據中抽出2組,求抽出的2組數據恰好是相鄰2天數據的概率;
(2)請根據所給五組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)根據(1)中所得的線性回歸方程,若天氣預報1月16日的白天平均氣溫![]() ,請預測該奶茶店這種飲料的銷量.
,請預測該奶茶店這種飲料的銷量.
(參考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸)、一位居民的月用水量不超過
(噸)、一位居民的月用水量不超過![]() 的部分按平價收費,超出
的部分按平價收費,超出![]() 的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.
的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)求直方圖中a的值;
(Ⅱ)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數,并說明理由;
(Ⅲ)若該市政府希望使85%的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值,并說明理由.
的值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() R.
R.
(1)證明:當![]() 時,函數
時,函數![]() 是減函數;
是減函數;
(2)根據![]() 的不同取值,討論函數
的不同取值,討論函數![]() 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(3)當![]() ,且
,且![]() 時,證明:對任意
時,證明:對任意![]() ,存在唯一的
,存在唯一的![]() R,使得
R,使得![]() ,且
,且![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com