
【題目】已知函數(shù)![]() ,曲線在點
,曲線在點![]() 處的切線方程為
處的切線方程為![]() .
.
![]() 求a,b的值;
求a,b的值;
![]() 2
2![]() 若當
若當![]() 時,關(guān)于x的不等式
時,關(guān)于x的不等式![]() 恒成立,求k的取值范圍.
恒成立,求k的取值范圍.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)求得![]() 的導(dǎo)數(shù),可得切線的斜率,由已知切線的方程可得切點,由
的導(dǎo)數(shù),可得切線的斜率,由已知切線的方程可得切點,由![]() ,
,![]() 的方程,可得
的方程,可得![]() ,
,![]() 的值;
的值;
(2)由題意可得![]() 恒成立,即有
恒成立,即有![]() 對
對![]() 恒成立,求導(dǎo)并根據(jù)函數(shù)單調(diào)性情況進行分類討論,最終獲得k取值范圍.
恒成立,求導(dǎo)并根據(jù)函數(shù)單調(diào)性情況進行分類討論,最終獲得k取值范圍.
解:![]() 函數(shù)
函數(shù)![]() ,
,
導(dǎo)數(shù)為![]() ,
,
曲線在點![]() 處的切線方程為
處的切線方程為![]() ,
,
可得![]() ,
,![]() ,則
,則![]() ,
,
即有![]() ,
,![]() ;
;
![]() 2
2![]() 當
當![]() 時,關(guān)于x的不等式
時,關(guān)于x的不等式![]() 恒成立,
恒成立,
可得![]() 恒成立,
恒成立,
即有![]() 對
對![]() 恒成立,
恒成立,
可設(shè)![]() ,
,
導(dǎo)數(shù)為![]() ,
,
設(shè)![]() ,
,![]() ,
,
![]() ,
,
當![]() 時,
時,![]() ,
,![]() 在
在![]() 遞增,可得
遞增,可得![]() ,
,
則![]() 在
在![]() 遞增,
遞增,![]() ,與題設(shè)矛盾;
,與題設(shè)矛盾;
當![]() ,
,![]() ,可得
,可得![]() ,
,
![]() 當
當![]() 時,
時,![]() ,在
,在![]() 時,
時,![]() ,
,![]() 遞減,可得
遞減,可得![]() ,
,
則![]() 在
在![]() 遞減,可得
遞減,可得![]() 恒成立;
恒成立;
![]() 當
當![]() 時,
時,![]() ,在
,在![]() 上
上![]() 遞增,
遞增,
在![]() 遞減,且
遞減,且![]() ,
,
所以在![]() 上
上![]() ,故在
,故在![]() 上
上![]() 遞增,
遞增,
![]() ,與題設(shè)矛盾.
,與題設(shè)矛盾.
綜上可得,k的范圍是![]()


 互動課堂系列答案
互動課堂系列答案 激活思維智能訓(xùn)練課時導(dǎo)學(xué)練系列答案
激活思維智能訓(xùn)練課時導(dǎo)學(xué)練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】黃岡市的天氣預(yù)報顯示,大別山區(qū)在今后的三天中,每一天有強濃霧的概率為![]() ,現(xiàn)用隨機模擬的方法估計這三天中至少有兩天有強濃霧的概率:先利用計算器產(chǎn)生
,現(xiàn)用隨機模擬的方法估計這三天中至少有兩天有強濃霧的概率:先利用計算器產(chǎn)生![]() 之間整數(shù)值的隨機數(shù),并用0,1,2,3,4,5表示沒有強濃霧,用6,7,8,9表示有強濃霧,再以每3個隨機數(shù)作為一組,代表三天的天氣情況,產(chǎn)生了如下20組隨機數(shù):
之間整數(shù)值的隨機數(shù),并用0,1,2,3,4,5表示沒有強濃霧,用6,7,8,9表示有強濃霧,再以每3個隨機數(shù)作為一組,代表三天的天氣情況,產(chǎn)生了如下20組隨機數(shù):
779 537 113 730 588 506 027 394 357 231
683 569 479 812 842 273 925 191 978 520
則這三天中至少有兩天有強濃霧的概率近似為![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在某公司舉行的年終慶典活動中,主持人利用隨機抽獎軟件進行抽獎:由電腦隨機生成一張如圖所示的3![]() 3表格,其中1格設(shè)獎300元,4格各設(shè)獎200元,其余4格各設(shè)獎100元,點擊某一格即顯示相應(yīng)金額.某人在一張表中隨機不重復(fù)地點擊3格,記中獎的總金額為X元.
3表格,其中1格設(shè)獎300元,4格各設(shè)獎200元,其余4格各設(shè)獎100元,點擊某一格即顯示相應(yīng)金額.某人在一張表中隨機不重復(fù)地點擊3格,記中獎的總金額為X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及數(shù)學(xué)期望
的概率分布及數(shù)學(xué)期望![]() .
.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 為矩形,直線
為矩形,直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
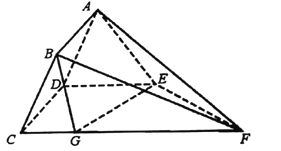
(1)求證:直線![]() 平面
平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上,且
上,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (其中
(其中![]() ,
,![]() 為自然對數(shù)的底數(shù),
為自然對數(shù)的底數(shù),![]() ).
).
(1)若![]() ,求函數(shù)
,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)證明:當![]() 時,函數(shù)
時,函數(shù)![]() 有兩個零點
有兩個零點![]() ,且
,且![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市十所重點中學(xué)進行高三聯(lián)考,共有5000名考生,為了了解數(shù)學(xué)學(xué)科的學(xué)習(xí)情況,現(xiàn)從中隨機抽出若干名學(xué)生在這次測試中的數(shù)學(xué)成績,制成如下頻率分布表:
分組 | 頻數(shù) | 頻率 |
| ① | ② |
|
| |
|
| |
| 36 |
|
|
| |
| 12 | ③ |
|
| |
合計 | ④ |

(1)根據(jù)上面頻率分布表,推出①,②,③,④處的數(shù)值分別為 , , , ;
(2)在所給的坐標系中畫出區(qū)間![]() 上的頻率分布直方圖;
上的頻率分布直方圖;
(3)根據(jù)題中信息估計總體:
(i)120分及以上的學(xué)生數(shù);
(ii)平均分;
(iii)成績落在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓C:![]() 的離心率為
的離心率為![]() ,其右焦點到橢圓C外一點
,其右焦點到橢圓C外一點![]() 的距離為
的距離為![]() ,不過原點O的直線l與橢圓C相交于A,B兩點,且線段AB的長度為2.
,不過原點O的直線l與橢圓C相交于A,B兩點,且線段AB的長度為2.
![]() 1
1![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 2
2![]() 求
求![]() 面積S的最大值.
面積S的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 中,
中,![]() ,且
,且![]() .
.
(1)求證:![]() 是等比數(shù)列,并求數(shù)列
是等比數(shù)列,并求數(shù)列![]() 的通項公式;
的通項公式;
(2)數(shù)列![]() 中是否存在不同的三項按照一定順序重新排列后,構(gòu)成等差數(shù)列?若存在,求滿足條件的項;若不存在,說明理由.
中是否存在不同的三項按照一定順序重新排列后,構(gòu)成等差數(shù)列?若存在,求滿足條件的項;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() (a為常數(shù),且
(a為常數(shù),且![]() )在
)在![]() 處取得極值.
處取得極值.
(1)求實數(shù)a的值,并求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)關(guān)于x的方程![]() 在
在![]() 上恰有1個實數(shù)根,求實數(shù)b的取值范圍;
上恰有1個實數(shù)根,求實數(shù)b的取值范圍;
(3)求證:當![]() 時,
時,![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com