
【題目】過直線2x+y+4=0和圓x2+y2+2x﹣4y+1=0的交點,且面積最小的圓方程為( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】若直線![]() 與曲線
與曲線![]() 滿足下列兩個條件:①直線
滿足下列兩個條件:①直線![]() 在點
在點![]() 處與曲線
處與曲線![]() 相切;②曲線
相切;②曲線![]() 在點
在點![]() 附近位于直線
附近位于直線![]() 的兩側,則稱直線
的兩側,則稱直線![]() 在點
在點![]() 處“切過”曲線
處“切過”曲線![]() .則下列結論正確的是( )
.則下列結論正確的是( )
A.直線![]() 在點
在點![]() 處“切過”曲線
處“切過”曲線![]()
B.直線![]() 在點
在點![]() 處“切過”曲線
處“切過”曲線![]()
C.直線![]() 在點
在點![]() 處“切過”曲線
處“切過”曲線![]()
D.直線![]() 在點
在點![]() 處“切過”曲線
處“切過”曲線![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三邊BC,CA,AB的中點分別是D(5,3),E(4,2),F(1,1).
(1)求△ABC的邊AB所在直線的方程及點A的坐標;
(2)求△ABC的外接圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為調研學校師生的環境保護意識,決定在本市所有學校中隨機抽取60所進行環境綜合考評成績達到80分以上(含80分)為達標.60所學校的考評結果頻率分布直方圖如圖所示(其分組區間為[50,60),[60,70),[70,80),[80,90),[90,100]).

(Ⅰ)試根據樣本估汁全市學校環境綜合考評的達標率;
(Ⅱ)若考評成績在[90.100]內為優秀.且甲乙兩所學校考評結果均為優秀從考評結果為優秀的學校中隨機地抽取兩所學校作經驗交流報告,求甲乙兩所學校至少有一所被選中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三邊BC,CA,AB的中點分別是D(5,3),E(4,2),F(1,1).
(1)求△ABC的邊AB所在直線的方程及點A的坐標;
(2)求△ABC的外接圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,圓![]() ,
,![]() 是圓M內一個定點,P是圓上任意一點,線段PN的垂直平分線l和半徑MP相交于點Q,當點P在圓M上運動時,點Q的軌跡為曲線E.
是圓M內一個定點,P是圓上任意一點,線段PN的垂直平分線l和半徑MP相交于點Q,當點P在圓M上運動時,點Q的軌跡為曲線E.
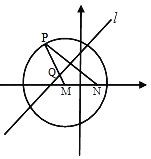
(1)求曲線E的方程;
(2)已知拋物線![]() 上,是否存在直線m與曲線E交于G,H,使得G,H中點F落在直線y=2x上,并且與拋物線相切,若直線m存在,求出直線m的方程,若不存在,說明理由.
上,是否存在直線m與曲線E交于G,H,使得G,H中點F落在直線y=2x上,并且與拋物線相切,若直線m存在,求出直線m的方程,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知點![]() 是拋物線
是拋物線![]() 上一定點,直線
上一定點,直線![]() 的傾斜角互補,且與拋物線另交于
的傾斜角互補,且與拋物線另交于![]() ,
,![]() 兩個不同的點.
兩個不同的點.

(1)求點![]() 到其準線的距離;
到其準線的距離;
(2)求證:直線![]() 的斜率為定值.
的斜率為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com