
【題目】已知函數![]() ,若
,若![]() 是函數
是函數![]() 的唯一極值點,則實數
的唯一極值點,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:由f(x)的導函數形式可以看出ex﹣kx=0在(0,+∞)無變號零點,
令g(x)=ex﹣kx,g′(x)=ex﹣k,需要對k進行分類討論來確定導函數為0時的根.
詳解:∵函數![]() 的定義域是(0,+∞),
的定義域是(0,+∞),
∴f′(x)=![]() .
.
x=1是函數f(x)的唯一一個極值點
∴x=1是導函數f′(x)=0的唯一根.
∴ex﹣kx=0在(0,+∞)無變號零點,
令g(x)=ex﹣kx
g′(x)=ex﹣k
①k≤0時,g′(x)>0恒成立.g(x)在(0,+∞)時單調遞增的
g(x)的最小值為g(0)=1,g(x)=0無解
②k>0時,g′(x)=0有解為:x=lnk
0<x<lnk時,g′(x)<0,g(x)單調遞減
lnk<x時,g′(x)>0,g(x)單調遞增
∴g(x)的最小值為g(lnk)=k﹣klnk
∴k﹣klnk>0
∴k<e,
由y=ex和y=ex圖象,它們切于(1,e),
綜上所述,k≤e.
故答案為:A.


科目:高中數學 來源: 題型:
【題目】對某校高三年級學生參加社區服務次數進行統計,隨機抽取![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖:
名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖:
分組 | 頻數 | 頻率 |
|
|
|
| 24 |
|
| 4 | 0.1 |
| 2 | 0.05 |
合計 |
| 1 |
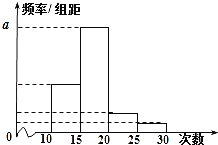
(1)求出表中![]() ,
,![]() 及圖中
及圖中![]() 的值;
的值;
(2)若該校高三學生有240人,試估計該校高三學生參加社區服務的次數在區間![]() 內的人數;
內的人數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,求至多一人參加社區服務次數在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某種書籍每冊的成本費![]() (元)與印刷冊數
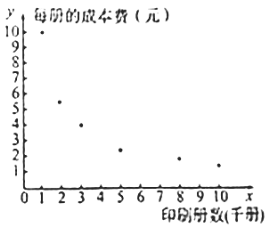
(元)與印刷冊數![]() (千冊)的數據作了初步處理,得到下面的散點圖及一些統計量的值.
(千冊)的數據作了初步處理,得到下面的散點圖及一些統計量的值.
|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
其中![]() ,
,![]() .
.
為了預測印刷![]() 千冊時每冊的成本費,建立了兩個回歸模型:
千冊時每冊的成本費,建立了兩個回歸模型:![]() ,
,![]() .
.
(1)根據散點圖,你認為選擇哪個模型預測更可靠?(只選出模型即可)
(2)根據所給數據和(1)中的模型選擇,求![]() 關于
關于![]() 的回歸方程,并預測印刷
的回歸方程,并預測印刷![]() 千冊時每冊的成本費.
千冊時每冊的成本費.
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為: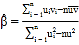 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
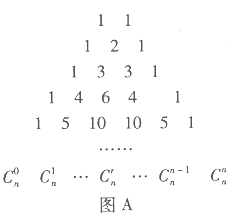
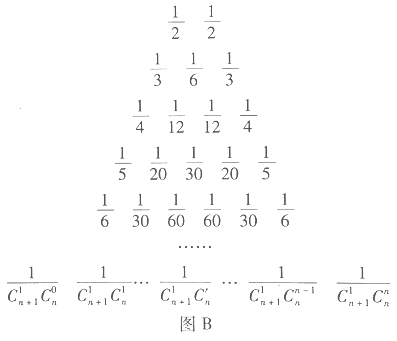
【題目】在我國南宋數學家楊輝所著的《詳解九章算法》(1261年)一書中,用如圖![]() 所示的三角形,解釋二項和的乘方規律.在歐洲直到1623年以后,法國數學家布萊士帕斯卡的著作(1655年)介紹了這個三角形,近年來,國外也逐漸承認這項成果屬于中國,所以有些書上稱這是“中國三角形”
所示的三角形,解釋二項和的乘方規律.在歐洲直到1623年以后,法國數學家布萊士帕斯卡的著作(1655年)介紹了這個三角形,近年來,國外也逐漸承認這項成果屬于中國,所以有些書上稱這是“中國三角形”![]() ,如圖
,如圖![]() .17世紀德國數學家萊布尼茨發現了“萊布尼茨三角形”,如圖
.17世紀德國數學家萊布尼茨發現了“萊布尼茨三角形”,如圖![]() .在楊輝三角中,相鄰兩行滿足關系式:
.在楊輝三角中,相鄰兩行滿足關系式:![]() ,其 中
,其 中![]() 是行數,
是行數,![]() .請類比上式,在萊布尼茨三角形中相鄰兩行滿足的關系式是__________.
.請類比上式,在萊布尼茨三角形中相鄰兩行滿足的關系式是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高一年級學生某次身體素質體能測試的原始成績采用百分制,已知所有這些學生的原始成績均分布在![]() 內,發布成績使用等級制.各等級劃分標準見下表.
內,發布成績使用等級制.各等級劃分標準見下表.
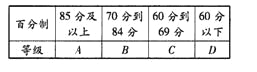
規定:![]() 三級為合格等級,D為不合格等級.為了解該校高一年級學生身體素質情況,從中抽取了
三級為合格等級,D為不合格等級.為了解該校高一年級學生身體素質情況,從中抽取了![]() 名學生的原始成績作為樣本進行統計.按照
名學生的原始成績作為樣本進行統計.按照![]() 的分組作出頻率分布直方圖如圖1所示,樣本中分數在80分及以上的所有數據的莖葉圖如圖2所示.
的分組作出頻率分布直方圖如圖1所示,樣本中分數在80分及以上的所有數據的莖葉圖如圖2所示.
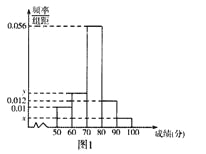
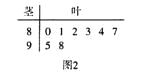
(I)求![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值,并估計該校高一年級學生成績是合格等級的概率;
的值,并估計該校高一年級學生成績是合格等級的概率;
(II)在選取的樣本中,從![]() 兩個等級的學生中隨機抽取2名學生進行調研,求至少有一名學生是
兩個等級的學生中隨機抽取2名學生進行調研,求至少有一名學生是![]() 等級的概率.
等級的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},且A∩B={2}.
(1)求a的值及集合A,B;
(2)設全集U=A∪B,求(UA)∪(UB);
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中點,已知AB=2,AD=2 ![]() ,PA=2,求:
,PA=2,求: 
(1)三角形PCD的面積;
(2)異面直線BC與AE所成的角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保護環境,某單位采用新工藝,把二氧化硅轉化為一種可利用的化工產品.已知該單位每月都有處理量,且處理量最多不超過![]() 噸,月處理成本
噸,月處理成本![]() (元)與月處理量
(元)與月處理量![]() (噸)之間的函數關系可近似的表示為:
(噸)之間的函數關系可近似的表示為:![]() ,且每處理一噸二氧化硅得到可利用的化工產品價值為
,且每處理一噸二氧化硅得到可利用的化工產品價值為![]() 元.
元.
(1)設該單位每月獲利為![]() (元),試將
(元),試將![]() 表示月處理
表示月處理![]() (噸)的函數;
(噸)的函數;
(2)若要保證該單位每月不虧損,則每月處理量應控制在什么范圍?
(3)該單位每月處理量為多少噸時,才能使每噸的平均處理成本最低?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com