Question

【題目】無窮數列滿足：為正整數，且對任意正整數，為前項、、、中等于的項的個數.

（1）若，求和的值；

（2）已知命題 存在正整數，使得，判斷命題的真假并說明理由；

（3）若對任意正整數，都有恒成立，求的值.

Answer 1

【答案】（1），；（2）真命題，證明見解析；（3）.

【解析】

（1）根據題意直接寫出、、的值，可得出結果；

（2）分和兩種情況討論，找出使得等式成立的正整數，可得知命題為真命題；

（3）先證明出“”是“存在，當時，恒有成立”的充要條件，由此可得出，然后利用定義得出，由此可得出的值.

（1）根據題意知，對任意正整數，為前項、、、中等于的項的個數，

因此，，，；

（2）真命題，證明如下：

①當時，則，，，此時，當時，；

②當時，設，則，，，

此時，當時，.

綜上所述，命題為真命題；

（3）先證明：“”是“存在，當時，恒有成立”的充要條件.

假設存在，使得“存在，當時，恒有成立”.

則數列的前項為，，

，，

，，

后面的項順次為，

，

，

，

故對任意的，

，

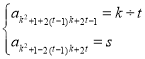對任意的，取，其中表示不超過的最大整數，則，

令，則，此時，

有，這與矛盾，

故若存在，當時，恒有成立，必有；從而得證.

另外：當時，數列為，

故，則.