
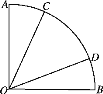
【題目】如圖所示,在圓心角為90°的扇形AOB中,以圓心O作為起點作射線OC,OD,則使∠AOC+∠BOD<45°的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根據題意得到試驗的全部結果所構成的區域為Ω={(x,y)|0≤x≤90,0≤y≤90},事件A表示∠AOC+∠BOD<45°,則其所構成的區域為A={(x,y)|x+y<45,0≤x≤90,0≤y≤90},由幾何概型的公式得到概率P(A)=![]()

設∠AOC=x°,∠BOD=y°,把(x,y)看作坐標平面上的點,則試驗的全部結果所構成的區域為Ω={(x,y)|0≤x≤90,0≤y≤90},若事件A表示∠AOC+∠BOD<45°,則其所構成的區域為A={(x,y)|x+y<45,0≤x≤90,0≤y≤90},即圖中的陰影部分,故面積S陰影=![]() ×45×45.由幾何概型的概率公式,得所求概率P(A)=
×45×45.由幾何概型的概率公式,得所求概率P(A)=![]()
故答案為:C.


科目:高中數學 來源: 題型:
【題目】在5件產品中,有3件一等品和2件二等品,從中任取2件,以![]() 為概率的事件是( )
為概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)是定義在R上的偶函數,對于x∈R,都有f(x+4)=f(x)+f(2)成立,當x1 , x2∈[0,2]且x1≠x2時,都有 ![]() <0,給出下列四個命題:
<0,給出下列四個命題:
①f(﹣2)=0;
②直線x=﹣4是函數y=f(x)的圖象的一條對稱軸;
③函數y=f(x)在[4,6]上為增函數;
④函數y=f(x)在(﹣8,6]上有四個零點.
其中所有正確命題的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=kx3+3(k﹣1)x2﹣k2+1在x=0,x=4處取得極值.
(1)求常數k的值;
(2)求函數f(x)的單調區間與極值;
(3)設g(x)=f(x)+c,且x∈[﹣1,2],g(x)≥2c+1恒成立,求c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三年級數學競賽初賽考試后,對90分以上(含90分)的成績進行統計,其頻率分布直方圖如圖所示,已知成績在130~140分數段的人數為2.
(1)求這組數據的平均數M.
(2)現根據初賽成績從第一組和第五組(從低分段至高分段依次為第一組、第二組、…、第五組)中任意選出兩人,形成幫扶小組.若選出的兩人的成績之差大于20,則稱這兩人為“黃金搭檔組”,試求選出的兩人為“黃金搭檔組”的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=﹣x2+bln(x+1)在[0,+∞)上單調遞減,則b的取值范圍( )
A.[0,+∞)
B.[﹣ ![]() ,+∞)
,+∞)
C.(﹣∞,0]
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() .
.
(1)若函數f(x)在區間(a,a+ ![]() )(a>0)上存在極值點,求實數a的取值范圍;
)(a>0)上存在極值點,求實數a的取值范圍;
(2)當x≥1時,不等式f(x)≥ ![]() 恒成立,求實數k的取值范圍.
恒成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是正方形.點E是棱PC的中點,平面ABE與棱PD交于點F.
(Ⅰ)求證:AB∥EF;
(Ⅱ)若PA=AD,且平面PAD⊥平面ABCD,求證:AF⊥平面PCD.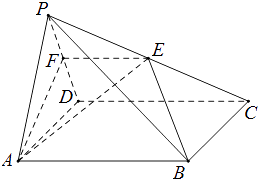
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com