
【題目】小明在石家莊市某物流派送公司找到了一份派送員的工作,該公司給出了兩種日薪薪酬方案.甲方案:底薪100元,每派送一單獎勵1元;乙方案:底薪140元,每日前55單沒有獎勵,超過55單的部分每單獎勵12元.
(1)請分別求出甲、乙兩種薪酬方案中日薪![]() (單位:元)與送貨單數
(單位:元)與送貨單數![]() 的函數關系式;
的函數關系式;
(2)根據該公司所有派送員100天的派送記錄,發現派送員的日平均派送單數與天數滿足以下表格:
日均派送單數 | 52 | 54 | 56 | 58 | 60 |
頻數(天) | 20 | 30 | 20 | 20 | 10 |
回答下列問題:
①根據以上數據,設每名派送員的日薪為![]() (單位:元),試分別求出這100天中甲、乙兩種方案的日薪
(單位:元),試分別求出這100天中甲、乙兩種方案的日薪![]() 平均數及方差;
平均數及方差;
②結合①中的數據,根據統計學的思想,幫助小明分析,他選擇哪種薪酬方案比較合適,并說明你的理由.
(參考數據: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
【答案】(1)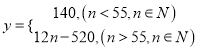 ;(2)見解析
;(2)見解析
【解析】試題分析:(1)甲方案:底薪100元,每派送一單獎勵1元;乙方案:底薪140元,每日前55單沒有獎勵,超過55單的部分每單獎勵12元. 求出甲、乙兩種薪酬方案中日薪![]() (單位:元)與送貨單數
(單位:元)與送貨單數![]() 的函數關系式;
的函數關系式;
①、由表格可知,甲方案中,日薪為152元的有20天,日薪為154元的有30天,日薪為156元的有20天,日薪為158元的有20天,日薪為160元的有10天,由此可求出這100天中甲方案的日薪![]() 平均數及方差:同理可求出這100天中乙兩種方案的日薪
平均數及方差:同理可求出這100天中乙兩種方案的日薪![]() 平均數及方差,
平均數及方差,
②不同的角度可以有不同的答案
試題解析:((1)甲方案中派送員日薪![]() (單位:元)與送貨單數
(單位:元)與送貨單數![]() 的函數關系式為:
的函數關系式為: ![]() ,
,
乙方案中派送員日薪![]() (單位:元)與送單數
(單位:元)與送單數![]() 的函數關系式為:
的函數關系式為:
![]() ,
,
(2)①、由表格可知,甲方案中,日薪為152元的有20天,日薪為154元的有30天,日薪為156元的有20天,日薪為158元的有20天,日薪為160元的有10天,則
![]()
![]() ,
,
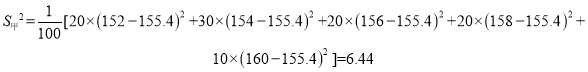 ,
,
乙方案中,日薪為140元的有50天,日薪為152元的有20天,日薪為176元的有20天,日薪為200元的有10天,則
![]()
![]() ,
,
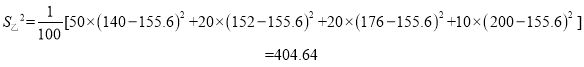
②、答案一:
由以上的計算可知,雖然![]() ,但兩者相差不大,且
,但兩者相差不大,且![]() 遠小于
遠小于![]() ,即甲方案日薪收入波動相對較小,所以小明應選擇甲方案.
,即甲方案日薪收入波動相對較小,所以小明應選擇甲方案.
答案二:
由以上的計算結果可以看出, ![]() ,即甲方案日薪平均數小于乙方案日薪平均數,所以小明應選擇乙方案.
,即甲方案日薪平均數小于乙方案日薪平均數,所以小明應選擇乙方案.
【題型】解答題
【結束】
20
【題目】已知橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
, ![]() ,且離心率為
,且離心率為![]() ,
, ![]() 為橢圓上任意一點,當
為橢圓上任意一點,當![]() 時,
時, ![]() 的面積為1.
的面積為1.
(1)求橢圓![]() 的方程;
的方程;
(2)已知點![]() 是橢圓
是橢圓![]() 上異于橢圓頂點的一點,延長直線
上異于橢圓頂點的一點,延長直線![]() ,
, ![]() 分別與橢圓交于點
分別與橢圓交于點![]() ,
, ![]() ,設直線
,設直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,求證:
,求證: ![]() 為定值.
為定值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)設![]() 由題
由題 ,由此求出
,由此求出![]() ,可得橢圓
,可得橢圓![]() 的方程;
的方程;
(2)設![]() ,
, ![]() ,
,
當直線![]() 的斜率不存在時,可得
的斜率不存在時,可得![]() ;
;
當直線![]() 的斜率不存在時,同理可得
的斜率不存在時,同理可得![]() .
.
當直線![]() 、
、![]() 的斜率存在時,
的斜率存在時,![]() ,
,
設直線![]() 的方程為
的方程為![]() ,則由
,則由 消去
消去![]() 通過運算可得
通過運算可得
 ,同理可得
,同理可得 ,由此得到直線
,由此得到直線![]() 的斜率為
的斜率為![]() ,
,
![]() 直線
直線![]() 的斜率為
的斜率為![]() ,進而可得
,進而可得![]() .
.
試題解析:(1)設![]() 由題
由題 ,
,
解得![]() ,則
,則![]() ,
,
![]() 橢圓
橢圓![]() 的方程為
的方程為![]() .
.
(2)設![]() ,
, ![]() ,
,
當直線![]() 的斜率不存在時,設
的斜率不存在時,設 ,則
,則 ,
,
直線![]() 的方程為
的方程為![]() 代入
代入![]() ,可得
,可得![]() ,
,
![]() ,
, ![]() ,則
,則 ,
,
![]() 直線
直線![]() 的斜率為
的斜率為 ,直線
,直線![]() 的斜率為
的斜率為![]() ,
,
 ,
,
當直線![]() 的斜率不存在時,同理可得
的斜率不存在時,同理可得![]() .
.
當直線![]() 、
、![]() 的斜率存在時,
的斜率存在時,![]() ,
,
設直線![]() 的方程為
的方程為![]() ,則由
,則由 消去
消去![]() 可得:
可得:
![]() ,
,
又![]() ,則
,則![]() ,代入上述方程可得
,代入上述方程可得
![]() ,
,
![]() ,則
,則![]()
 ,
,
設直線![]() 的方程為
的方程為![]() ,同理可得
,同理可得 ,
,
![]() 直線
直線![]() 的斜率為
的斜率為 ,
,
![]() 直線
直線![]() 的斜率為
的斜率為![]() ,
,
![]()
 .
.
所以,直線![]() 與
與![]() 的斜率之積為定值
的斜率之積為定值![]() ,即
,即![]() .
.


科目:高中數學 來源: 題型:
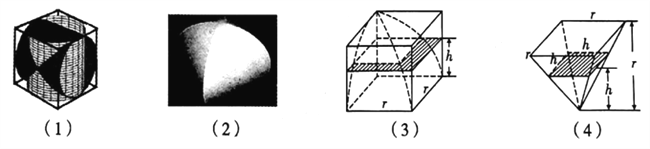
【題目】中國古代數學家劉徽在《九章算術注》中,稱一個正方體內兩個互相垂直的內切圓柱所圍成的立體為“牟合方蓋”,如圖(1)(2),劉徽未能求得牟合方蓋的體積,直言“欲陋形措意,懼失正理”,不得不說“敢不闕疑,以俟能言者”.約200年后,祖沖之的兒子祖暅提出“冪勢既同,則積不容異”,后世稱為祖暅原理,即:兩等高立體,若在每一等高處的截面積都相等,則兩立體體積相等.如圖(3)(4),祖暅利用八分之一正方體去掉八分之一牟合方蓋后的幾何體與長寬高皆為八分之一正方體的邊長的倒四棱錐“等冪等積”,計算出牟合方蓋的體積,據此可知,牟合方蓋的體積與其外切正方體的體積之比為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
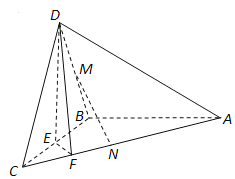
【題目】如圖,在三棱錐![]() 中,已知
中,已知![]() 是正三角形,
是正三角形, ![]() 平面
平面![]() 為
為![]() 的中點,
的中點, ![]() 在棱
在棱![]() 上,且
上,且![]() .
.
(1)求三棱錐![]() 的體積;
的體積;
(2)求證: ![]() 平面
平面![]() ;
;
(3)若![]() 為
為![]() 中點,
中點, ![]() 在棱
在棱![]() 上,且
上,且![]() ,求證:
,求證: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,設AB1的中點為D,B1C∩BC1=E.

求證:(1)DE∥平面AA1C1C;
(2)BC1⊥AB1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() 且函數
且函數![]() ,若函數f(x)的圖象上兩個相鄰的對稱軸距離為
,若函數f(x)的圖象上兩個相鄰的對稱軸距離為![]() .
.
(1)求函數f(x)的解析式;
(2)將函數y=f(x)的圖象向左平移![]() 個單位后,得到函數y=g(x)的圖象,求函數g(x)的表達式并其對稱軸;
個單位后,得到函數y=g(x)的圖象,求函數g(x)的表達式并其對稱軸;
(3)若方程f(x)=m(m>0)在![]() 時,有兩個不同實數根x1,x2,求實數m的取值范圍,并求出x1+x2的值.
時,有兩個不同實數根x1,x2,求實數m的取值范圍,并求出x1+x2的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
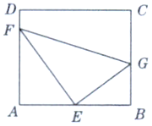
【題目】如圖,某污水處理廠要在個矩形ABCD的池底水平鋪設污水凈化管道(![]() ,E是直角頂點)來處理污水,管道越長,污水凈化效果越好,設計要求管道的接口E是AB的中點,F、G分別落在AD、BC上,且
,E是直角頂點)來處理污水,管道越長,污水凈化效果越好,設計要求管道的接口E是AB的中點,F、G分別落在AD、BC上,且![]() ,
,![]() ,設
,設![]() .
.
(1)試將污水管道的長度l表示成![]() 的函數,并寫出定義域;
的函數,并寫出定義域;
(2)當![]() 為何值時,污水凈化效果最好,并求此時管道的長度.
為何值時,污水凈化效果最好,并求此時管道的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學運算是指在明晰運算對象的基礎上,依據運算法則解決數學問題的素養.因為運算,數的威力無限;沒有運算,數就只是一個符號.對數運算與指數冪運算是兩類重要的運算.
(1)對數的運算性質降低了運算的級別,簡化了運算,在數學發展史上是偉大的成就.對數運算性質的推導有很多方法.請同學們根據所學知識推導如下的對數運算性質:如果![]() ,且
,且![]() ,
,![]() ,那么
,那么![]() ;
;
(2)請你運用上述對數運算性質計算![]() 的值;
的值;
(3)因為![]() ,所以
,所以![]() 的位數為4(一個自然數數位的個數,叫做位數).請你運用所學過的對數運算的知識,判斷
的位數為4(一個自然數數位的個數,叫做位數).請你運用所學過的對數運算的知識,判斷![]() 的位數.(注
的位數.(注![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com