
【題目】如圖所示,我國某海岸線可看作由圓弧AB和射線BC連接而成,其中圓弧AB所在圓O的半徑為12海里,圓心角為120°,規(guī)定外輪除特許外,不得進(jìn)入離我國海岸線12海里以內(nèi)的區(qū)域.在港口A處設(shè)有觀察站,外輪一旦進(jìn)入規(guī)定區(qū)域,觀察站會接收到預(yù)警信號,現(xiàn)從A處測得一外輪在北偏東60°,距離港口x海里的P處,沿直線PA方向航行.
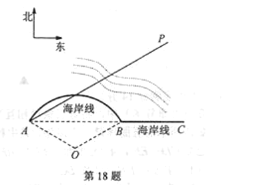
(1)當(dāng)x=30時,分別求出外輪到海岸線BC和弧AB的最短距離,并判斷觀察站是否接收到預(yù)警信號?
(2)當(dāng)x為何值時,觀察站開始接收到預(yù)警信號?
【答案】(1)最短距離為6![]() 12,不能接收到預(yù)警信號;(2)6+6
12,不能接收到預(yù)警信號;(2)6+6![]()
【解析】
(1)根據(jù)已知條件求出點![]() 到射線
到射線![]() 的距離,和到圓弧
的距離,和到圓弧![]() 的最小值,再與12海里進(jìn)行比較即可得判斷;
的最小值,再與12海里進(jìn)行比較即可得判斷;
(2)由(1)知 ![]() 到弧
到弧![]() 的距離比
的距離比![]() 到射線
到射線![]() 的距離小,所以只要列出點
的距離小,所以只要列出點![]() 到圓弧
到圓弧![]() 的最小值為
的最小值為![]() 的關(guān)系式即可求
的關(guān)系式即可求![]() 的值.
的值.
(1)以![]() 為坐標(biāo)原點,建立如圖所示的直角坐標(biāo)系,
為坐標(biāo)原點,建立如圖所示的直角坐標(biāo)系,

當(dāng)![]() 時,由直角三角形中
時,由直角三角形中![]() ,可得
,可得![]() 到
到![]() 的距離為
的距離為![]() ,
,
此時![]() 即
即![]() ,可得P到弧
,可得P到弧![]() 的最短距離為
的最短距離為
![]() ,可得判斷觀察站不能接收到預(yù)警信號;
,可得判斷觀察站不能接收到預(yù)警信號;
(2)當(dāng)![]() 到弧
到弧![]() 的距離為
的距離為![]() ,由于
,由于![]() 到
到![]() 的距離大于
的距離大于![]() ,
,
設(shè)![]() ,可得
,可得 ,且
,且![]() ,
,
可得![]() ,即有
,即有![]() ,
,
解得![]() (負(fù)的舍去),
(負(fù)的舍去),
當(dāng)![]() 為
為![]() 海里時,觀察站開始接收到預(yù)警信號.
海里時,觀察站開始接收到預(yù)警信號.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】下面幾種推理過程是演繹推理的是( )
A. 某校高三有8個班,1班有51人,2班有53人,3班有52人,由此推測各班人數(shù)都超過50人
B. 由三角形的性質(zhì),推測空間四面體的性質(zhì)
C. 平行四邊形的對角線互相平分,菱形是平行四邊形,所以菱形的對角線互相平分
D. 在數(shù)列![]() 中,
中,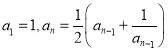 ,可得
,可得![]() ,由此歸納出
,由此歸納出![]() 的通項公式
的通項公式![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)點![]() 是拋物線
是拋物線![]() 上的動點,
上的動點,![]() 是
是![]() 的準(zhǔn)線上的動點,直線
的準(zhǔn)線上的動點,直線![]() 過
過![]() 且與
且與![]() (
(![]() 為坐標(biāo)原點)垂直,則點
為坐標(biāo)原點)垂直,則點![]() 到
到![]() 的距離的最小值的取值范圍是( )
的距離的最小值的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() ,
,![]() 是兩條不同的直線,
是兩條不同的直線,![]() ,
,![]() ,
,![]() 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若![]() ,
,![]() ,則
,則![]()
②若![]() ,
,![]() ,
,![]() ,則
,則![]()
③若![]() ,
,![]() ,則
,則![]()
④若![]() ,
,![]() ,則
,則![]()
其中正確命題的序號是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() 是拋物線
是拋物線![]() 上一點,
上一點,![]() 為
為![]() 的焦點.
的焦點.
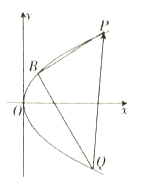
(1)若![]() ,
,![]() 是
是![]() 上的兩點,證明:
上的兩點,證明:![]() ,
,![]() ,
,![]() 依次成等比數(shù)列.
依次成等比數(shù)列.
(2)過![]() 作兩條互相垂直的直線與
作兩條互相垂直的直線與![]() 的另一個交點分別交于
的另一個交點分別交于![]() ,
,![]() (
(![]() 在
在![]() 的上方),求向量
的上方),求向量![]() 在
在![]() 軸正方向上的投影的取值范圍.
軸正方向上的投影的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一位幼兒園老師給班上k(k≥3)個小朋友分糖果.她發(fā)現(xiàn)糖果盒中原有糖果數(shù)為a0,就先從別處抓2塊糖加入盒中,然后把盒內(nèi)糖果的![]() 分給第一個小朋友;再從別處抓2塊糖加入盒中,然后把盒內(nèi)糖果的
分給第一個小朋友;再從別處抓2塊糖加入盒中,然后把盒內(nèi)糖果的![]() 分給第二個小朋友;…,以后她總是在分給一個小朋友后,就從別處抓2塊糖放入盒中,然后把盒內(nèi)糖果的
分給第二個小朋友;…,以后她總是在分給一個小朋友后,就從別處抓2塊糖放入盒中,然后把盒內(nèi)糖果的![]() 分給第n(n=1,2,3,…k)個小朋友.如果設(shè)分給第n個小朋友后(未加入2塊糖果前)盒內(nèi)剩下的糖果數(shù)為an.
分給第n(n=1,2,3,…k)個小朋友.如果設(shè)分給第n個小朋友后(未加入2塊糖果前)盒內(nèi)剩下的糖果數(shù)為an.
(1)當(dāng)k=3,a0=12時,分別求a1,a2,a3;
(2)請用an-1表示an;令bn=(n+1)an,求數(shù)列{bn}的通項公式;
(3)是否存在正整數(shù)k(k≥3)和非負(fù)整數(shù)a0,使得數(shù)列{an}(n≤k)成等差數(shù)列,如果存在,請求出所有的k和a0,如果不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系xOy中直線![]() 與拋物線C:
與拋物線C:![]() 交于A,B兩點,且
交于A,B兩點,且![]() .
.
![]() 求C的方程;
求C的方程;
![]() 若D為直線
若D為直線![]() 外一點,且
外一點,且![]() 的外心M在C上,求M的坐標(biāo).
的外心M在C上,求M的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com