Question

【題目】已知函數是偶函數．

（1）求k的值；

（2）若方程有實數根，求b的取值范圍；

（3）設，若函數與的圖象有且只有一個公共點，求實數a的取值范圍．

Answer 1

【答案】（1）（2）（3）

【解析】

（1）根據函數的奇偶性得， 代入函數的解析式中，利用對數的運算法則得到 ；（2）將函數代入方程，將方程轉化為兩個函數交點的問題；通過判斷函數 的單調性，得到其最小值，從而求得b的取值范圍為 ；（3）由題意，兩個函數圖像有且只有一個公共點即方程有且只有一個實數根；通過討論方程根的情況來求得參數的取值范圍.

（1）∵為偶函數，∴，有，

∴對恒成立．

∴對恒成立，

∴

對恒成立，∴．

（2）由題意知，有實數根，即有解．

令，則函數的圖象與直線有交點，

．

∵，∴，

∴b的取值范圍是．

（3）由（1）知，，

∴由題意知有且只有一個實數根．

令，則，則關于t的方程（*）有且只有一個正根．

若，則，不合題意，舍去；

若，則方程（*）的兩根異號或方程有兩相等正根．

方程（*）有兩相等正根等價于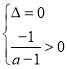，可解得．

方程（*）的兩根異號等價于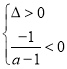，可解得．

綜上所述，實數a的取值范圍是．