
【題目】已知函數(shù)![]() .
.
(1)判斷![]() 的單調(diào)性,并說明理由;
的單調(diào)性,并說明理由;
(2)判斷![]() 的奇偶性,并用定義證明;
的奇偶性,并用定義證明;
(3)若不等式![]() 對任意
對任意![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)增函數(shù),理由見解析 (2)奇函數(shù),證明見解析 (3)![]()
【解析】
(1)利用函數(shù)單調(diào)性的定義即可得證.
(2)首先判斷定義域關(guān)于原點對稱,利用函數(shù)奇偶性定義即可得證.
(3)由(1)(2)以及分離參數(shù)法將不等式轉(zhuǎn)化為![]() 對任意
對任意![]() 恒成立,令
恒成立,令![]() ,求
,求![]() 的最大值即可.
的最大值即可.
解:(1)![]() 是定義域
是定義域![]() 上的增函數(shù).
上的增函數(shù).
設(shè)任意的![]() ,且
,且![]() ,則
,則
![]() ,
,
因為![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]()
即![]() ,所以
,所以![]() 是定義域
是定義域![]() 上的增函數(shù).
上的增函數(shù).
(2)![]() 是奇函數(shù).
是奇函數(shù).
證明:因為![]() ,定義域
,定義域![]() 關(guān)于原點對稱
關(guān)于原點對稱
所以對任意![]() ,都有
,都有![]()
所以![]() 是奇函數(shù).
是奇函數(shù).
(3)由(2)知![]() 為
為![]() 上的奇函數(shù),所以不等式
上的奇函數(shù),所以不等式![]() 對任意
對任意![]() 恒成立,等價于
恒成立,等價于![]() 對任意
對任意![]() 恒成立.
恒成立.
又由(1)知,![]() 在定義域
在定義域![]() 上單調(diào)遞增,
上單調(diào)遞增,
得![]() 對任意
對任意![]() 恒成立即
恒成立即![]() 對任意
對任意![]() 恒成立.
恒成立.
設(shè)![]() ,
,
則![]() ,故
,故![]() 在
在![]() 上的最大值為
上的最大值為![]() ,
,
所以實數(shù)![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】 (1)已知正數(shù)a,b滿足a+b=1,求證:a2+b2≥![]() ;
;
(2)設(shè)a、b、c為△ABC的三條邊,求證:a2+b2+c2<2(ab+bc+ca).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某高中學(xué)校高一年級學(xué)生某次身體素質(zhì)體能測試的原始成績采用百分制,已知所有這些學(xué)生的原始成績均分布在[50,100]內(nèi),發(fā)布成績使用等級制.各等級劃分標(biāo)準(zhǔn)見圖表.規(guī)定:A,B,C三級為合格等級,D為不合格等級.
分數(shù) | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等級 | A | B | C | D |
為了解該校高一年級學(xué)生身體素質(zhì)情況,從中抽取了n名學(xué)生的原始成績作為樣本進行統(tǒng)計.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分組作出頻率分布直方圖如圖①所示,樣本中原始成績在80分及以上的所有數(shù)據(jù)的莖葉圖如圖②所示.
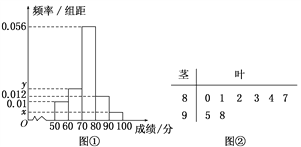
(1)求n和頻率分布直方圖中的x,y的值,并估計該校高一年級學(xué)生成績是合格等級的概率;
(2)在選取的樣本中,從成績?yōu)?/span>A,D兩個等級的學(xué)生中隨機抽取2名學(xué)生進行調(diào)研,求至少有一名學(xué)生的成績是A等級的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司今年年初用25萬元引進一種新的設(shè)備,投入設(shè)備后每年收益為21萬元.該公司第![]() 年需要付出設(shè)備的維修和工人工資等費用
年需要付出設(shè)備的維修和工人工資等費用![]() 的信息如下圖.
的信息如下圖.
(1)求![]() ;
;
(2)引進這種設(shè)備后,從第幾年開始該公司能夠獲利?
(3)這種設(shè)備使用多少年,該公司的年平均獲利最大?

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,其中
,其中![]() ,
,![]() ,
,![]() 為常數(shù).
為常數(shù).
(1)若![]() ,
,![]() ,試討論函數(shù)
,試討論函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 在
在![]() 上單調(diào)遞增,且
上單調(diào)遞增,且![]() ,證明:
,證明:![]() ,并求
,并求![]() 的最小值(用
的最小值(用![]() ,
,![]() 的代數(shù)式表示).
的代數(shù)式表示).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠生產(chǎn)某種產(chǎn)品的年固定成本為200萬元,每生產(chǎn)![]() 千件,需另投入成本為
千件,需另投入成本為![]() ,當(dāng)年產(chǎn)量不足80千件時,
,當(dāng)年產(chǎn)量不足80千件時,![]() (萬元).當(dāng)年產(chǎn)量不小于80千件時,
(萬元).當(dāng)年產(chǎn)量不小于80千件時,![]() (萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產(chǎn)的商品能全部售完.
(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產(chǎn)的商品能全部售完.
(1)寫出年利潤![]() (萬元)關(guān)于年產(chǎn)量
(萬元)關(guān)于年產(chǎn)量![]() (千件)的函數(shù)解析式;
(千件)的函數(shù)解析式;
(2)當(dāng)年產(chǎn)量為多少千件時,該廠在這一商品的生產(chǎn)中所獲利潤最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于一個具有正南正北、正東正西方向規(guī)則布局的城鎮(zhèn)街道,從一點到另一點的距離是在南北方向上行進的距離加上在東西方向上行進的距離,這種距離即“曼哈頓距離”,也叫“出租車距離”.對于平面直角坐標(biāo)系中的點![]() 和
和![]() ,兩點間的“曼哈頓距離”
,兩點間的“曼哈頓距離”![]() .
.

(1)如圖,若![]() 為坐標(biāo)原點,
為坐標(biāo)原點,![]() ,
,![]() 兩點坐標(biāo)分別為
兩點坐標(biāo)分別為![]() 和
和![]() ,求
,求![]() ,
,![]() ,
,![]() ;
;
(2)若點![]() 滿足
滿足![]() ,試在圖中畫出點
,試在圖中畫出點![]() 的軌跡,并求該軌跡所圍成圖形的面積;
的軌跡,并求該軌跡所圍成圖形的面積;
(3)已知函數(shù)![]() ,試在
,試在![]() 圖象上找一點
圖象上找一點![]() ,使得
,使得![]() 最小,并求出此時點
最小,并求出此時點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,函數(shù)
,函數(shù)![]() .
.
(1)若函數(shù)![]() ,
,![]() 最小值為
最小值為![]() ,求實數(shù)
,求實數(shù)![]() 的值;
的值;
(2)當(dāng)![]() 時,不等式
時,不等式![]() 的解集為
的解集為![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com