
【題目】若函數 ![]() ,則( )
,則( )
A.最大值為1,最小值為 ![]()
B.最大值為1,無最小值
C.最小值為 ![]() ,無最大值
,無最大值
D.既無最大值也無最小值查看解析
【答案】D
【解析】解答: ![]() ,令
,令 ![]() ,得想x<0或x>1,令
,得想x<0或x>1,令 ![]() ,得
,得 ![]() ,因此函數
,因此函數 ![]() 在
在 ![]() 上單調遞增,在(0,1)上單調遞減,在(1,+
上單調遞增,在(0,1)上單調遞減,在(1,+ ![]() )上單調遞增,所以在x=0時,函數
)上單調遞增,所以在x=0時,函數 ![]() 取得極大值1,在x=1時,函數
取得極大值1,在x=1時,函數 ![]() 取得極小值
取得極小值 ![]() ,但是函數
,但是函數 ![]() 在(-
在(- ![]() ,+
,+ ![]() )上,既無最大值也無最小值,弄清楚極值與最值是兩個不同的概念,就不會選錯答案,此處選擇D.分析:弄清楚極值與最值是兩個不同的概念.
)上,既無最大值也無最小值,弄清楚極值與最值是兩個不同的概念,就不會選錯答案,此處選擇D.分析:弄清楚極值與最值是兩個不同的概念.
【考點精析】本題主要考查了函數的最大(小)值與導數的相關知識點,需要掌握求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值才能正確解答此題.
比較,其中最大的是一個最大值,最小的是最小值才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】對于函數f(x)給出定義:
設f′(x)是函數y=f(x)的導數,f″(x)是函數f′(x)的導數,若方程f″(x)=0有實數解x0 , 則稱點(x0 , f(x0))為函數y=f(x)的“拐點”.
某同學經過探究發現:任何一個三次函數f(x)=ax3+bx2+cx+d(a≠0)都有“拐點”;任何一個三次函數都有對稱中心,且“拐點”就是對稱中心.給定函數 ![]() ,請你根據上面探究結果,計算
,請你根據上面探究結果,計算![]() = .
= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某少數民族的刺繡有著悠久的歷史,如圖(1),(2),(3),(4)為最簡單的四個圖案,這些圖案都是由小正方形構成,小正方形數越多刺繡越漂亮.現按同樣的規律刺繡(小正方形的擺放規律相同),設第n個圖形包含f(n)個小正方形. 
(1)求出f(5)的值.
(2)利用合情推理的“歸納推理思想”,歸納出f(n+1)與f(n)之間的關系式,并根據你得到的關系式求出f(n)的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】省環保研究所對某市市中心每天環境放射性污染情況進行調查研究后,發現一天中環境綜合放射性污染指數![]() 與時刻
與時刻![]() (時)的關系為
(時)的關系為 ,其中
,其中![]() 是與氣象有關的參數,且
是與氣象有關的參數,且![]() ,若用每天
,若用每天![]() 的最大值為當天的綜合放射性污染指數,并記作
的最大值為當天的綜合放射性污染指數,并記作![]() .
.
(1)令![]() .求
.求![]() 的取值范圍;
的取值范圍;
(2)求![]() ;
;
(3)省政府規定,每天的綜合放射性污染指數不得超過2,試問目前該市市中心的綜合放射性污染指數是否超標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經銷商經銷某種農產品,在一個銷售季度內,每售出![]() 該產品獲利潤500元,未售出的產品,每
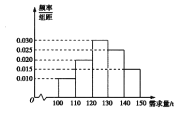
該產品獲利潤500元,未售出的產品,每![]() 虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了
虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了![]() 該農產品.以
該農產品.以![]() (單位:
(單位: ![]() )表示下一個銷售季度內的市場需求量,
)表示下一個銷售季度內的市場需求量, ![]() (單位:元)表示下一個銷售季度內經銷該農產品的利潤.
(單位:元)表示下一個銷售季度內經銷該農產品的利潤.
(1)將![]() 表示為
表示為![]() 的函數;
的函數;
(2)根據直方圖估計利潤![]() 不少于57000元的概率;
不少于57000元的概率;
(3)在直方圖的需求量分組中,以各組的區間中點值代表該組的各個值,并以需求量落入該區間的頻率作為需求量取該區間中點值的概率(例如:若需求量![]() ,則取
,則取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的頻率),求
的頻率),求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】市環保局舉辦2013年“六五”世界環境日宣傳活動,進行現場抽獎.抽獎規則是:盒中裝有10張大小相同的精美卡片,卡片上分別印有“環保會徽”或“綠色環保標志”圖案.參加者每次從盒中抽取卡片兩張,若抽到兩張都是“綠色環保標志”卡即可獲獎.
(1)活動開始后,一位參加者問:盒中有幾張“綠色環保標志”卡?主持人笑說:我只知道若從盒中抽兩張都不是“綠色環保標志”卡的概率是 ![]() .求抽獎者獲獎的概率;
.求抽獎者獲獎的概率;
(2)現有甲乙丙丁四人依次抽獎,抽后放回,另一人再抽.用ξ表示獲獎的人數.求ξ的分布列及E(ξ),D(ξ).
查看答案和解析>>
科目:高中數學 來源: 題型:
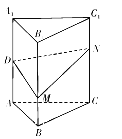
【題目】如圖,正三棱柱![]() 的各條棱長均相等,
的各條棱長均相等, ![]() 為
為![]() 的中點,
的中點, ![]() 分別是線段
分別是線段![]() 和線段
和線段![]() 上的動點(含端點),且滿足
上的動點(含端點),且滿足![]() .當
.當![]() 運動時,下列結論中不正確的是( )
運動時,下列結論中不正確的是( )
A. 平面![]() 平面
平面![]() B. 三棱錐
B. 三棱錐![]() 的體積為定值
的體積為定值
C. ![]() 可能為直角三角形 D. 平面
可能為直角三角形 D. 平面![]() 與平面
與平面![]() 所成的銳二面角范圍為
所成的銳二面角范圍為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,以原點為圓心,橢圓C的短半軸長為半徑的圓與直線x﹣y+2=0相切.
,以原點為圓心,橢圓C的短半軸長為半徑的圓與直線x﹣y+2=0相切. 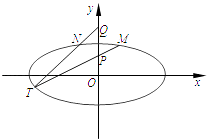
(1)求橢圓C的方程;
(2)已知點P(0,1),Q(0,2).設M,N是橢圓C上關于y軸對稱的不同兩點,直線PM與QN相交于點T,求證:點T在橢圓C上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com