
【題目】如圖,在三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 在線段
在線段![]() 上,
上, ![]() ,
, ![]() .
.
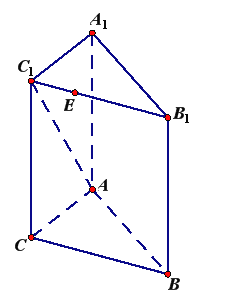
(1)求證: ![]() ;
;
(2)試探究:在![]() 上是否存在點
上是否存在點![]() ,滿足
,滿足![]() 平面
平面![]() ,若存在,請指出點
,若存在,請指出點![]() 的位置,并給出證明;若不存在,說明理由.
的位置,并給出證明;若不存在,說明理由.
【答案】(1)證明見解析;(2)答案見解析.
【解析】試題分析:(1)因為![]() 面
面![]() ,所以
,所以![]() ,結合
,結合![]() 就有
就有![]() 面
面![]() ,從而
,從而![]() .(2)取
.(2)取![]() ,在平面
,在平面![]() 內過
內過![]() 作
作![]() 交
交![]() 于
于![]() ,連結
,連結![]() .可以證明四邊形
.可以證明四邊形![]() 為平行四邊形,從而
為平行四邊形,從而![]() ,也就是
,也就是![]() 平面
平面![]() .我們還可以在平面
.我們還可以在平面![]() 內過
內過![]() 作
作![]() ,交
,交![]() 于
于![]() ,連結
,連結![]() .通過證明平面
.通過證明平面![]() 平面
平面![]() 得到
得到![]() 平面
平面![]() .
.
解析:(1)∵![]() 面
面![]() ,
, ![]() 面
面![]() ,∴
,∴![]() .又∵
.又∵![]() ,
, ![]() ,
, ![]() 面
面![]() ,
, ![]() ,∴
,∴![]() 面
面![]() ,又
,又![]() 面
面![]() ,∴
,∴![]() .
.
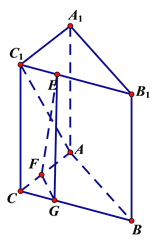
(2)(法一)當![]() 時,
時, ![]() 平面
平面![]() .
.
理由如下:在平面![]() 內過
內過![]() 作
作![]() 交
交![]() 于
于![]() ,連結
,連結![]() .∵
.∵![]() ,∴
,∴![]() ,又
,又![]() ,且
,且![]() ,∴
,∴![]() 且
且![]() ,∴四邊形
,∴四邊形![]() 為平行四邊形,∴
為平行四邊形,∴![]() ,又
,又![]() 面
面![]() ,
, ![]() 面
面![]() ,∴
,∴![]() 平面
平面![]() .
.
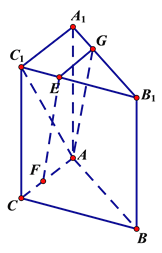
(法二)當![]() 時,
時, ![]() 平面
平面![]() .理由如下:在平面
.理由如下:在平面![]() 內過
內過![]() 作
作![]() ,交
,交![]() 于
于![]() ,連結
,連結![]() .∵
.∵![]() ,
, ![]() 面
面![]() ,
, ![]() 面
面![]() ,
,
∴![]() 平面
平面![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,又
,又![]() 面
面![]() ,
, ![]() 面
面![]() ,∴
,∴![]() 平面
平面![]() .又
.又![]() 面
面![]() ,
, ![]() 面
面![]() ,
, ![]() ,∴平面
,∴平面![]() 平面
平面![]() .∵
.∵![]() 面
面![]() ,∴
,∴![]() 平面
平面![]() .
.


科目:高中數學 來源: 題型:
【題目】某桶裝水經營部每天的房租、人員工資等固定成本為200元,每桶水的進價為5元,銷售單價與日均銷售量的關系如圖所示.
銷售單價/元 | … | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | … |
日均銷售量/桶 | … | 480 | 460 | 440 | 420 | 400 | 380 | … |
請根據以上數據作出分析,這個經營部怎樣定價才能獲得最大利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解適齡公務員對開放生育二胎政策的態度,某部門隨機調查了90位三十歲到四十歲的公務員,得到如下列聯表,因不慎丟失部分數據.
(1)完成表格數據,判斷是否有99%以上的把握認為“生二胎意愿與性別有關”并說明理由;
(2)已知15位有意愿生二胎的女性公務員中有兩位來自省婦聯,該部門打算從這15位有意愿生二胎的女性公務員中隨機邀請兩位來參加座談,設邀請的2人中來自省婦聯的人數為X,求X的分布列及數學期望E(X).
男性公務員 | 女性公務員 | 總計 | |
有意愿生二胎 | 15 | 45 | |
無意愿生二胎 | 25 | ||
總計 |
P(k2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
附: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從參加高二年級期末考試的學生中隨機抽取60名學生,將其數學成績(均為整數)分成六段[40,50),[50,60),…,[90,100]后得到如下頻率分布表.根據相關信息回答下列問題: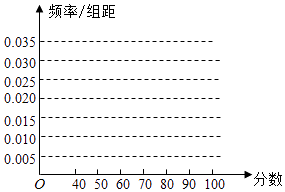
(1)求a,b的值,并畫出頻率分布直方圖;
(2)統計方法中,同一組數據常用該組區間的中點值作為代表,據此估計本次考試的平均分;
(3)用分層抽樣的方法在分數在[60,80)內學生中抽取一個容量為6的樣本,將該樣本看成一個總體,從中任取2人,求至多有1人的分數在[70,80)內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={1,3,5,7},B={x|(2x﹣1)(x﹣5)>0},則A∩(RB)( )
A.{1,3}
B.{1,3,5}
C.{3,5}
D.{3,5,7}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種商品的市場需求量![]() (萬件)、市場供應量
(萬件)、市場供應量![]() (萬件)與市場價格
(萬件)與市場價格![]() (元/件)分別近似地滿足下列關系:
(元/件)分別近似地滿足下列關系: ![]() ,
, ![]() .當
.當![]() 時的市場價格稱為市場平衡價格,此時的需求量稱為平衡需求量.
時的市場價格稱為市場平衡價格,此時的需求量稱為平衡需求量.
(1)求平衡價格和平衡需求量;
(2)若該商品的市場銷售量![]() (萬件)是市場需求量
(萬件)是市場需求量![]() 和市場供應量
和市場供應量![]() 兩者中的較小者,該商品的市場銷售額
兩者中的較小者,該商品的市場銷售額![]() (萬元)等于市場銷售量
(萬元)等于市場銷售量![]() 與市場價格
與市場價格![]() 的乘積.
的乘積.
①當市場價格![]() 取何值時,市場銷售額
取何值時,市場銷售額![]() 取得最大值;
取得最大值;
②當市場銷售額![]() 取得最大值時,為了使得此時的市場價格恰好是新的市場平衡價格,則政府應該對每件商品征稅多少元?
取得最大值時,為了使得此時的市場價格恰好是新的市場平衡價格,則政府應該對每件商品征稅多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線過點P(﹣3 ![]() ,4),它的漸近線方程為y=±
,4),它的漸近線方程為y=± ![]() x.
x.
(1)求雙曲線的標準方程;
(2)設F1和F2為該雙曲線的左、右焦點,點P在此雙曲線上,且|PF1||PF2|=41,求∠F1PF2的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com